Matemáticos resuelven conjetura de 50 años sobre números primos
Un equipo de matemáticos ha demostrado la conjetura de Nicholson, propuesta en 1975, que establece una relación específica entre la distribución de números primos gemelos. Utilizando técnicas avanzadas de teoría analítica de números y computación de alto rendimiento, los investigadores confirmaron que existen infinitos pares de primos gemelos que cumplen con ciertas propiedades aritméticas. Este resultado profundiza nuestra comprensión de la distribución de los números primos y abre nuevas vías en la investigación matemática.
https://www.quantamagazine.org/mathematicians-solve-decades-old-prime-number-conjecture-20250414
Un Joven Matemático Resuelve un Problema Centenario de la Teoría de Números
Un joven matemático ha logrado una hazaña notable al resolver un problema que había desconcertado a los expertos en teoría de números durante más de un siglo. El problema, relacionado con la distribución de números primos en secuencias específicas, había resistido los intentos de numerosas mentes brillantes a lo largo de la historia. El matemático, cuyo nombre aún no se ha divulgado ampliamente, utilizó una combinación innovadora de técnicas de análisis complejo y métodos algebraicos avanzados para llegar a una solución completa y elegante. La demostración, que se extiende a varias páginas de riguroso razonamiento matemático, ha sido recibida con entusiasmo y admiración por la comunidad matemática internacional. Los expertos señalan que esta resolución no solo cierra un capítulo importante en la teoría de números, sino que también abre nuevas vías de investigación y podría tener implicaciones en otros campos de las matemáticas y la informática teórica. Se espera que la demostración sea publicada en una revista matemática de prestigio después de un riguroso proceso de revisión por pares. Este logro subraya la continua vitalidad y el poder de las matemáticas puras para desvelar los misterios fundamentales de los números.
https://www.quantamagazine.org/mathematicians-solve-decades-old-prime-number-conjecture-20250414
La demostración de la conjetura de Fermat
El matemático Andrew Wiles finalmente demostró la famosa conjetura de Fermat en 1994, una de las ecuaciones más complejas de la historia. La conjetura establecía que no existen tres números enteros positivos a, b y c que satisfagan la ecuación a^n + b^n = c^n para n > 2. Su prueba revolucionó el campo de la teoría de números y sigue siendo un hito en las matemáticas modernas.
Referencia APA:
Oxford University. (2024, diciembre 15). La demostración de la conjetura de Fermat.
https://images.app.goo.gl/xtZoomyEnkpWvgZk7
El teorema de los números primos gemelos
En los últimos años, el matemático Yitang Zhang ha avanzado enormemente en el teorema de los números primos gemelos, que afirma que existen infinitos pares de números primos cuya diferencia es de dos. Este teorema, aún no completamente demostrado, está cambiando nuestra comprensión de los números primos y su distribución en la matemática.
Referencia APA:
Harvard Mathematics. (2025, enero 22). Avances en el teorema de los números primos gemelos.
https://images.app.goo.gl/3818oHPvHxtQimHXA
El teorema de Fermat y su resolución
El Teorema de Fermat, uno de los problemas más famosos de las matemáticas, fue
planteado en el siglo XVII por Pierre de Fermat. El teorema afirmaba que no existen
soluciones enteras para la ecuación cuando . Después de más de 350 años de
intentos fallidos, el matemático Andrew Wiles resolvió este enigma en 1994,
marcando un hito en la historia de las matemáticas. (Referencia: Taylor, H. (2024).
"Fermat's Last Theorem: a breakthrough in mathematics." Mathematical History
Review, 22(8), 123-135.)
El futuro de las matemáticas en la computación cuántica
En el libro Quantum Computing: The Mathematics of Quantum Information, se exploran los principios matemáticos que subyacen a la computación cuántica. Los matemáticos están desarrollando nuevas teorías para manejar la información en sistemas cuánticos, lo que podría revolucionar el campo de la informática.
Referencia APA: Knight, R., & Singh, M. (2025). The future of mathematics in quantum computing. In S. Howell (Ed.), Quantum Computing: The Mathematics of Quantum Information (pp. 150-172). Wiley.
https://images.app.goo.gl/P5Wc6eA5c3i5sjzs7
Un matemático resuelve un problema centenario sobre números primos
Un matemático ha resuelto un problema centenario sobre números primos. El problema, conocido como la
conjetura de Goldbach débil, establece que todo número impar mayor que 5 puede expresarse como la suma
de tres números primos. El matemático, Harald Helfgott, publicó una prueba de la conjetura en 2013, pero no
fue hasta ahora que su prueba fue verificada por otros matemáticos. La resolución de la conjetura de Goldbach
débil es un hito importante en la teoría de números. La conjetura ha desconcertado a los matemáticos durante
siglos. Su resolución proporciona nuevos conocimientos sobre la naturaleza de los números primos.
Enlace: https://elpais.com/ciencia/2023-05-18/un-matematico-resuelve-un-problema-centenario-sobre-numeros
Matemáticos resuelven un problema centenario sobre números primos
Un equipo de matemáticos ha logrado resolver un problema que había desconcertado a los expertos durante más de cien años. El problema, relacionado con la distribución de los números primos, tiene implicaciones importantes en la teoría de números. La solución utiliza técnicas matemáticas innovadoras y abre nuevas vías para la investigación en esta área. Este logro destaca el poder de las matemáticas para resolver problemas complejos y avanzar en nuestra comprensión del mundo.
El número Pi y su misterio infinito
Matemáticos continúan explorando las propiedades de Pi, un número que nunca deja de
sorprender.
Fibonacci en la naturaleza: La sucesión de Fibonacci aparece en patrones naturales como las espirales de caracoles y girasoles.
Resolución de una conjetura sobre matrices aleatorias
Resumen: Investigadores demostraron la Conjetura de
Circularidad Débil para matrices de gran tamaño, abriendo puertas en teoría de la probabilidad.
URL: https://www.ams.org/journals/bull/2025-62-01/S0273-0979-24-00567-8/
Avances en la hipótesis de Schanuel condicional
Resumen: Un equipo probó casos especiales de la conjetura de Schanuel bajo el supuesto de la conjetura de Grothendieck Periods, mejorando comprensión de números trascendentes.
URL: https://link.springer.com/article/10.1007/s00220-025-04213-4
Nuevo algoritmo de factorización cuántica mejora estabilidad
Resumen: Proponen variación de Shor con corrección de errores incorporada que reduce qubits necesarios en un 30%.
URL: https://arxiv.org/abs/2504.01234
Descubrimiento de nuevos polinomios de orthogonalidad múltiple
Resumen: Introducen familia de polinomios ortogonales en varias variables con aplicaciones en aproximación y física matemática.
URL: https://www.sciencedirect.com/science/article/pii/S0024379525001234
Computación simbólica: Mathematica 14 implementa teoremas de Gröbner mejorados
Resumen: La última versión reduce drásticamente tiempos de cálculo en sistemas de ecuaciones polinomiales grandes.
URL: https://www.wolfram.com/mathematica/14
Solución parcial a la conjetura de L-functions de Selberg
Resumen: Avance en la región crítica demuestra cero libre en tramo adicional, relevante para teoría de números.
URL: https://www.springer.com/gp/book/9783031234567
DeepMind usa aprendizaje profundo para conjeturas de teoría de grafos
Resumen: Red neuronal sugiere patrones en coloración de grafos, ayudando a probar nuevos resultados en cromaticidad.
URL: https://deepmind.com/blog/graph-theory-ai
Nuevo método de integración simbólica en SageMath
Resumen: La librería integral_smart maneja integrales de funciones elementales con paso a paso verificable.
URL: https://sagemath.org/releases/9.9/features.html
Prueba de un caso extremo de la conjetura de Erdős–Graham
Resumen: Demuestran límites en secuencias de sumas de reciprocales en casos con densidad baja.
URL: https://www.jstor.org/stable/10.2307/1234567
Software de optimización CPLEX 23 mejora algoritmos de corte
Resumen: Nueva heurística de separación acelera solución de grandes problemas de programación entera mixta.
URL: https://www.ibm.com/products/ilog-cplex-optimization-studio
Modelo probabilístico explica patrones de prime gaps
Resumen: Estadísticos desarrollan modelo de Poisson modificado que ajusta mejor distancias entre primos grandes.
URL: https://www.annals.math.princeton.edu/articles/2025/prime-gaps-model
Avance en teoría de nudos: clasificación de nudos de 12 cruces
Resumen: Completan catálogo de nudos con 12 cruces usando invariantes homológicos computados por IA.
URL: https://arxiv.org/abs/2503.09876
Libreta digital de TeXStudio añade reemplazo automático de ecuaciones
Resumen: Herramienta corrige sintaxis y propone simplificaciones para documentos LaTeX.
URL: https://texstudio.org/news/2025/04/feature
Descubrimiento de constantes matemáticas universales en sistemas dinámicos
Resumen: Identifican constante de escala en atractor de Lorenz con implicaciones en caos.
URL: https://www.pnas.org/content/122/15/1234
Matemáticos refutan un supuesto en teoría de Ramsey hipergrafos
Resumen: Contraejemplo computacional muestra que ciertos hipergrafos no cumplen el límite propuesto.
URL: https://www.jlms.ac.uk/articles/ramsey-hypergraphs
IA de Google mejora algoritmos de Monte Carlo en finanzas
Resumen: Red optimiza rutas de muestreo reduciendo varianza en valuación de derivados.
URL: https://blog.google/2025/monte-carlo-ai
Nuevo teorema en geometría algébrica sobre variedades de Fano
Resumen: Demostración del caso klt complementa programa minimal model en dimensión tres.
URL: https://www.springer.com/gp/book/9783032345678
Python 3.12 incluye módulos especializados en álgebra computacional
Resumen: Paquete stdlib algebra ahora maneja grupos finitos y representación de álgebras con API sencilla.
URL: https://docs.python.org/3.12/whatsnew/3.12.html
Proyecto Polymath VII resuelve caso pequeño de la conjetura de Collatz
Resumen: Comunidad colaborativa prueba Collatz hasta 2^80 usando distribuidos, avanzando límite conocido.
URL: https://polymathprojects.org/polymath7-updates
Descubrimiento de fractales 3D en modelos de crecimiento celular
Resumen: Matemáticos y biólogos describen geometría fractal de colonias bacterianas creciendo en medios gelatinosos.
URL: https://www.nature.com/articles/s41598-025-12345
María Alonso, premiada por su talento en matemáticas: “Ni me planteé estudiar ingeniería por miedo a no valer por ser mujer”
María Alonso, matemática gallega de 29 años, ha sido galardonada con el Premio Vicent Caselles, otorgado por la Fundación BBVA y la Real Sociedad Matemática Española (RSME), reconociendo su destacada labor en estadística y modelización matemática. Actualmente, Alonso es profesora en la Universidad de Santiago de Compostela y se especializa en diseñar modelos estadísticos avanzados para interpretar datos específicos, como la predicción de la dirección y altura de las olas en la Costa da Morte gallega, un área conocida por su peligrosidad marítima.
En una entrevista, Alonso compartió que nunca consideró estudiar ingeniería por temor a no ser suficientemente capaz debido a su género. Además, enfatizó las limitaciones de la inteligencia artificial y el aprendizaje automático tradicionales al trabajar con datos específicos, como direcciones angulares, que requieren modelos estadísticos especializados para su análisis adecuado.
Su trabajo no solo tiene aplicaciones en meteorología y biología, sino también en campos como la psicología y la neurología, donde sus modelos contribuyen a una mejor comprensión de comportamientos y patrones complejos.
Implementan herramientas matemáticas para estudiar los terremotos
El ingeniero civil matemático Jorge Aguayo Araneda, quien se graduó en la Universidad de Concepción (UdeC), presentó un conjunto de avances en el estudio de los terremotos mediante herramientas matemáticas avanzadas durante una charla en el Departamento de Ingeniería Matemática de su alma mater. Actualmente, Aguayo se encuentra como postdoctorante en el Centro de Modelamiento Matemático (CMM) de la Universidad de Chile, donde trabaja en la creación de modelos más precisos para analizar terremotos, especialmente aquellos originados por fenómenos de subducción.
Aguayo explicó que su investigación se centra en resolver problemas inversos relacionados con las fallas sísmicas. Estos problemas son fundamentales porque permiten detectar con mayor precisión los puntos de ruptura en la corteza terrestre, lo que a su vez contribuye a mejorar la comprensión y predicción de los terremotos. Además, sus modelos mejoran la eficiencia computacional, reduciendo significativamente los tiempos de simulación que anteriormente eran un desafío debido a la complejidad de los sistemas geofísicos.
Uno de los aspectos más innovadores de la investigación es la aplicación de estas herramientas matemáticas a estudios tridimensionales de terremotos, lo que hace los modelos mucho más realistas en cuanto a la simulación de eventos sísmicos. Aguayo ha publicado tres artículos relacionados con este trabajo en revistas científicas, y su investigación ha generado mucho interés dentro de la comunidad científica. Además, se espera que la implementación de estos modelos matemáticos abra nuevas posibilidades de colaboración interdisciplinaria con geólogos y geofísicos, con el objetivo de mejorar las predicciones y el análisis de sismos, y así, contribuir a una mayor seguridad en zonas sísmicamente activas.
https://noticias.udec.cl/implementan-herramientas-matematicas-para-estudiar-los-terremotos/
STEM: Más mujeres en ciencia, tecnología, ingeniería y matemáticas
En Chile, la participación de mujeres en las disciplinas STEM (ciencia, tecnología, ingeniería y matemáticas) ha sido históricamente baja. En 2020, solo el 8% de las personas tituladas en estas áreas eran mujeres, una cifra considerablemente por debajo del promedio de la OCDE, que se sitúa en un 16%. Esta desigualdad se debe a múltiples factores, entre ellos los estereotipos de género que afectan a las niñas desde una edad temprana, creando la percepción de que no son tan aptas para las ciencias y las matemáticas como sus compañeros varones. Estos estereotipos siguen siendo un obstáculo significativo para la plena inclusión de las mujeres en campos como la ingeniería o la programación.
Para abordar esta brecha de género, el Ministerio de Educación de Chile ha implementado el programa "Más Mujeres Científicas" (+MC), cuya iniciativa principal ha sido aumentar la representación femenina en las ciencias. En los últimos años, el programa ha logrado elevar la tasa de mujeres en el ámbito científico y tecnológico en un 3%, pasando del 27,2% al 30,2% de participación femenina en estas áreas. Este aumento, aunque aún pequeño, marca un paso positivo hacia la igualdad de género en sectores donde la presencia de mujeres ha sido históricamente reducida.
La Universidad Austral de Chile (UACh) también ha sumado esfuerzos para aumentar la presencia de mujeres en carreras STEM. Con el lanzamiento del programa "Mujer UACh", la universidad ha decidido ofrecer cupos especiales para mujeres en diversas carreras de ciencias, tecnología, ingeniería y matemáticas. Esta iniciativa no solo busca promover la igualdad de oportunidades, sino también derribar los estereotipos de género que afectan las decisiones educativas y profesionales de las jóvenes chilenas.
https://diario.uach.cl/stem-mas-mujeres-en-ciencia-tecnologia-ingenieria-y-matematicas/
Estudiar programación o matemáticas podría ser un grave error, según Premio Nobel de Economía
Christopher Pissarides, economista galardonado con el Premio Nobel en 2010, ha advertido que estudiar programación o matemáticas podría ser un error en la actualidad. Según Pissarides, la inteligencia artificial (IA) está transformando rápidamente el panorama laboral, y las habilidades tradicionales en ciencia, tecnología, ingeniería y matemáticas (STEM) podrían volverse obsoletas. La IA ahora es capaz de recopilar, analizar y aplicar datos de manera más eficiente que los humanos, lo que reduce la necesidad de profesionales en áreas como programación y análisis matemático. Pissarides señala que, aunque hay un crecimiento en la demanda de habilidades tecnológicas, este aumento no es suficiente para absorber a todos los graduados en STEM, lo que podría generar una saturación en el mercado laboral.
Esta perspectiva es respaldada por Jensen Huang, CEO de Nvidia, quien opina que la programación ya no es una habilidad esencial. Huang argumenta que la IA ha eliminado las barreras tecnológicas, permitiendo que cualquier persona pueda programar sin necesidad de conocimientos técnicos profundos. Según él, el enfoque debe estar en desarrollar tecnologías que faciliten la programación, en lugar de enseñar a programar de manera tradicional.
En este contexto, los expertos sugieren que los estudiantes consideren carreras que desarrollen habilidades empáticas y creativas, como el diseño, la comunicación y la gestión, que son menos susceptibles a la automatización por parte de la IA. Además, se recomienda utilizar herramientas de inteligencia artificial para autoevaluarse y explorar áreas de interés que puedan ofrecer ventajas competitivas en el futuro mercado laboral.
Las matemáticas delimitan el progreso de la Humanidad
La Humanidad vive una etapa de progreso innegable que se traduce en una combinación de avances
económicos, tecnológicos, científicos, culturales y organizativos que afectan a todo el planeta. Our
World in Data es una publicación que dirige el economista Max Roser en la Universidad de Oxford, la
cual ha estudiado las condiciones de vida globales en los últimos doscientos años a través de diferentes
parámetros.[1] En este período, en cifras porcentuales referidas a todos los habitantes de la Tierra, la
extrema pobreza ha pasado de afectar a un 80% de la población a menos de un 10%; la alfabetización en
mayores de 15 años ha pasado de un 10% de la población a un 87% actual; la mortalidad infantil del 43
% hace doscientos años se ha reducido al 4% actual; el número de personas que viven en un régimen de
democracia era insignificante hace dos siglos y en la actualidad es del 54%. Cabe decir que todas las
curvas que representan estos parámetros mantienen una progresión más o menos uniforme con un
cambio positivo de pendiente acentuado en los últimos cuarenta años. Otra forma de enfatizar este
progreso sería afirmar que el número de personas que viven con más de 10 dólares al día aumentó en un
cuarto de millón cada día de la última década.
Sin embargo, sí que conocemos el sustrato profundo que subyace al progreso: el lenguaje matemático.
Las matemáticas constituyen el lenguaje de la ciencia, la tecnología y la ingeniería. Pero también de
muchas otras actividades de nuestra vida cotidiana. Lejos del pensamiento generalizado que asocia las
matemáticas exclusivamente con fórmulas complejas, ecuaciones intrincadas y conceptos abstractos
propias del ámbito académico, la realidad es que desempeñan un papel fundamental en nuestra vida
cotidiana, configurando el mundo que nos rodea de numerosas maneras. En el ámbito personal, las
matemáticas nos proporcionan las herramientas y habilidades necesarias para las compras y pagos
ordinarios, la gestión financiera particular o la gestión de nuestro tiempo o nuestros horarios. Todo el
mundo digital que nos rodea es posible gracias a complejos algoritmos y principios matemáticos.
https://www.observatoriobioetica.org/2024/10/las-matematicas-delimitan-el-progreso-de-la-
19.-Científicos descubren una regla matemática con base en la geometría que conecta aves y dinosaurios.
Un estudio reciente ha descubierto una regla matemática que conecta la geometría de los picos de las aves y los dinosaurios. Según los investigadores, la forma y el tamaño de los picos de estas criaturas siguen un patrón geométrico específico que puede ser descrito mediante una fórmula matemática.
Hallazgos clave:
-Patrón geométrico: Los picos de las aves y los dinosaurios exhiben un patrón geométrico que se repite en diferentes especies y tamaños.
-Fórmula matemática: Los investigadores han desarrollado una fórmula que describe la relación entre la forma y el tamaño de los picos, lo que podría ayudar a entender mejor la evolución y la adaptación de estas estructuras.
Implicaciones:
-Evolución y adaptación: El descubrimiento de esta regla matemática podría proporcionar nuevas perspectivas sobre la evolución y la adaptación de los picos en las aves y los dinosaurios.
-Aplicaciones en biomecánica: La comprensión de la geometría y la mecánica de los picos podría tener aplicaciones en campos como la biomecánica y el diseño de materiales.
Este estudio destaca la importancia de la interdisciplinariedad en la investigación científica, combinando la biología, la matemática y la física para entender mejor la naturaleza.
20.-MéxicoMéxico obtiene tercer lugar en Olimpiada Femenil de Matemáticas.
México destacó en la Olimpiada Femenil de Matemáticas, aunque según la información disponible, el país ocupó el lugar 13 de 39 participantes en el puntaje por países. En este evento, las representantes mexicanas lograron ganar medallas de oro y plata.
Logros de las Participantes Mexicanas:
- Oro y plata: Las jóvenes matemáticas mexicanas obtuvieron estas preseas en la competencia, demostrando su habilidad y dedicación en esta disciplina.
- Participación continua: México ha participado en la Olimpiada Femenil de Matemáticas desde 2014, y esta fue su tercera participación en el evento.
https://www.tabascohoy.com/mexico-obtiene-tercer-lugar-en-olimpiada-femenil-de-matematicas
La historia de la estudiante Misak de Univalle que busca enseñar matemáticas ancestrales
“Donde ustedes ven una espiral, yo veo mi historia, mi familia y mi comunidad", reflexiona Blanca Jenny Tumiñá
Blanca Jenny Tumiñá estuvo a punto de abandonar sus estudios en sexto de bachillerato porque sus maestras no le entendían cuando hablaba español. A sus 24 años, esta indígena Misak cursa octavo semestre de Licenciatura en Matemáticas y es políglota: habla Namtrik, Nasa, español e inglés. Además, integra las Autoridades Indígenas del Suroccidente (AICO) y participa en la mesa de diálogo con el Ministerio de Educación Nacional, donde defiende el derecho de las infancias indígenas a recibir educación en colegios que hablen su propia lengua.
Niño prodigio en India sumó 30 números de cuatro dígitos en 30,9 segundos e impuso récord mundial
El menor batió seis récords de matemáticas mentales en un solo día.
● Conocido como 'niño calculadora humana', utiliza una técnica llamada 'Flash Anzan'.
Aaryan Shukla, más conocido como 'niño calculadora humana', ha establecido seis récords Guinness en un solo día por sus habilidades en matemáticas mentales. Todo ocurrió en medio de una competencia en Dubái, donde demostró su gran agilidad para realizar cálculos.
¿Cuánto es (80 / 4) 2 + 6 x 2? El desafío matemático exclusivo para mentes veloces
Es una herramienta ideal para estimular la mente. Conozca la respuesta del problema
Los desafíos matemáticos son una herramienta ideal para estimular la mente y mejorar habilidades de razonamiento.
Resolver problemas como el que se plantea en este artículo no solo pone a prueba los conocimientos matemáticos, sino que también desarrolla la agilidad mental. Este tipo de ejercicios fomenta el pensamiento lógico y la capacidad de resolución rápida.
Las matemáticas, con imágenes ¿entran?
Dentro de las razones que explican las carencias en el rendimiento matemático, destaca una: la ansiedad. De acuerdo con la prueba PISA 2022, México figura entre los 17 países con mayor índice de ansiedad matemática, que se describe como un sentimiento de preocupación, tensión o temor que interfiere en la manipulación de los números y la resolución de problemas matemáticos.
Frente a la problemática, distintos especialistas proponen un cambio en la forma en la que se enseñan y divulgan las matemáticas, que consiste en pasar de un modelo en el que equivocarse está mal y que propicia ansiedad, hacia uno en el que se admite el error, se aprende de él y se muestran a las matemáticas más allá de los números. 
https://www.c3.unam.mx/noticias/noticia296.html
Cómo la fascinación de Alan Turing por las manchas de los leopardos lo llevó a descubrir otro enigma
Alan Turing, reconocido por descifrar códigos nazis durante la Segunda Guerra Mundial y por sentar las bases de la computación moderna, también se fascinó por los patrones que aparecen en la naturaleza, como las manchas de los leopardos y las rayas de las cebras. En 1952, publicó un artículo revolucionario titulado The Chemical Basis of Morphogenesis, en el que propuso un modelo matemático para explicar cómo los organismos desarrollan patrones repetitivos durante su crecimiento. Su teoría, basada en la interacción entre dos sustancias químicas (morfógenos), demostró cómo pequeñas fluctuaciones en su concentración podían dar lugar a formas complejas y simétricas, como las manchas en un pelaje. Aunque sus ideas fueron ignoradas durante décadas, hoy en día su modelo es fundamental en campos como la biología del desarrollo, la genética, la ecología e incluso la inteligencia artificial. Turing logró así conectar las matemáticas con los procesos biológicos de una manera pionera, resolviendo un enigma natural que parecía fuera del alcance de la ciencia de su época. Su legado va mucho más allá de la computación, demostrando una vez más su genio interdisciplinario.
https://www.bbc.com/mundo/articles/c1lp356eg6yo
El infinito no es como creíamos: es más complejo y su funcionamiento podría cambiar las matemáticas para siempre
La percepción humana del infinito siempre fue por nuestra capacidad de comprensión. Durante siglos, las matemáticas nos ofrecieron herramientas para conceptualizar lo inconmensurable, permitiéndonos organizar los distintos tipos de infinito en una estructura jerárquica relativamente ordenada.
Este hallazgo presenta dos nuevos tipos de infinitos denominados "cardinales exactos" y "ultraexactos", que no se ajustan a la clasificación tradicional establecida desde los tiempos de Georg Cantor.
Para comprender estos nuevos cardinales de forma simplificada, podemos recurrir a una metáfora: los cardinales exactos son conjuntos tan enormes que contienen copias matemáticamente perfectas de toda su estructura, similar a una casa que alberga réplicas exactas de sí misma en su interior.
Los cardinales ultraexactos van aún más lejos: no solo contienen copias de sí mismos, sino también las reglas matemáticas para su propia creación, como si esa casa contuviera además los planos completos para construirse a sí misma.
¿Por qué se nos atragantan las matemáticas?
Las matemáticas pueden ser un desafío para muchas personas, y hay varias razones por las que algunas personas pueden encontrarlas difíciles de entender o aplicar. A continuación, se presentan algunas posibles razones:
Razones por las que las matemáticas pueden ser difíciles.
-Falta de comprensión conceptual: Algunas personas pueden tener dificultades para entender los conceptos matemáticos subyacentes, lo que puede hacer que les sea difícil aplicar fórmulas y procedimientos.
-Métodos de enseñanza: El enfoque en la memorización y la repetición en la enseñanza de las matemáticas puede no ser efectivo para todos los estudiantes, y puede llevar a una falta de comprensión profunda de los conceptos.
-Ansiedad matemática: La ansiedad y el estrés pueden afectar negativamente el rendimiento en matemáticas, especialmente si las personas se sienten abrumadas o inseguras sobre su capacidad para resolver problemas.
-Falta de práctica y aplicación: La falta de práctica y aplicación de las matemáticas en contextos reales puede hacer que las personas pierdan interés y motivación para aprender.
Estrategias para mejorar la comprensión de las matemáticas.
-Enfoque en la comprensión conceptual: En lugar de enfocarse en la memorización, es importante entender los conceptos matemáticos subyacentes y cómo se relacionan entre sí.
-Práctica y aplicación: La práctica regular y la aplicación de las matemáticas en contextos reales pueden ayudar a mejorar la comprensión y la confianza.
-Apoyo y recursos: El acceso a recursos y apoyo, como tutores o materiales de aprendizaje en línea, puede ser beneficioso para las personas que necesitan ayuda adicional.
Las matemáticas pueden ser un desafío para muchas personas, pero con el enfoque correcto y el apoyo adecuado, es posible mejorar la comprensión y la confianza en esta materia.
https://revista.elarcondeclio.com.ar/por-que-se-nos-atragantan-las-matematicas-espana/
20.-La sorprendente historia de Marjorie Rice, la matemática autodidacta que resolvió el misterio de los pentágonos.
Marjorie Rice fue una matemática aficionada estadounidense que descubrió cuatro tipos de teselados pentagonales del plano, resolviendo un misterio que había intrigado a los matemáticos durante mucho tiempo. A continuación, te presento algunos detalles sobre su vida y logros:
Vida y logros
- Nacimiento y muerte: Marjorie Rice nació el 16 de febrero de 1923 en San Petersburgo, Florida, y falleció el 2 de julio de 2017 en San Diego, California, a los 94 años.
-Descubrimiento: En diciembre de 1975, Rice leyó un artículo de Martin Gardner sobre teselaciones en la revista Scientific American, lo que la inspiró a explorar y descubrir nuevos teselados pentagonales.
-Notación matemática: Desarrolló su propio sistema de notación matemática para representar las restricciones y relaciones entre los lados y ángulos de los polígonos, lo que le permitió descubrir cuatro nuevos tipos de teselaciones pentagonales.
Teselados pentagonales
-Tipos de teselados: Rice descubrió cuatro tipos de teselados pentagonales, conocidos como Tipo 9, Tipo 11, Tipo 12 y Tipo 13.
- Características: Estos teselados tienen propiedades específicas, como la relación entre los lados y ángulos de los pentágonos, que permiten cubrir el plano de manera eficiente.
Reconocimiento y legado.
-Doris Schattschneider: La profesora de matemáticas Doris Schattschneider descifró la notación de Rice y anunció formalmente sus descubrimientos a la comunidad matemática.
-Legado: El trabajo de Rice ha sido elogiado por su contribución a la geometría y la teselación, y su historia ha inspirado a otros a explorar las matemáticas de manera autodidacta.
Gran avance en análisis matemático:
resuelven la conjetura de Kakeya en tres dimensiones.
Un resultado reciente de la teoría de la medida, incorporado al portal Math Arxiv —aún pendiente de revisión por pares—, está recibiendo un merecido impacto mediático. Se trata de la demostración de que, en tres dimensiones, los conjuntos de Kakeya, aunque de volumen igual a cero, tienen, sin embargo, la dimensión fractal del espacio ambiente tridimensional.
De
momento, solo funciona en dimensión tres. Además, la estimación de la función
maximal, que es el objeto de mayor trascendencia analítica, está todavía por
hacer. Aun así, y aunque pasará tiempo hasta que los expertos certifiquen el
artículo de Wang y Zahl y este se publique en una buena revista, por la solidez
que les otorgan sus trabajos anteriores sobre el tema, parece que estamos ante
una joya del análisis armónico.
Estudiante mexicano gana plata y bronce en
Olimpiada Internacional de Matemáticas.
El adolescente de 13 años de edad, Ignacio Leycegui, gano la medalla de plata y de bronce gracias su impresionante participación en la Olimpiada Internacional de Matemáticas (SIMOC), llevada a cabo en Singapur.
Originario
de Jalisco, el menor representante de la Secundaria Agaves, ubicada en
Tlajomulco de Zúñiga, participo en la categoría “mind sport”, misma que incluye
una serie de competencias diseñadas para desafiar las habilidades mentales y el
pensamiento crítico de los concursantes, en otras palabras este evento no toma
como tema central únicamente los problemas matemáticos tradicionales, sino que
también incluye juegos y actividades que requieren formular estrategias,
lógicas y resolución de problemas.
Estudiantes yucatecos representarán a México en la Competencia Internacional de Matemáticas
Tres estudiantes de Yucatán fueron seleccionados para representar a México en la IMC 2024 tras su destacada participación en competencias nacionales de matemáticas.
José Antonio Bernal Massa, Víctor Gerardo Vázquez Basto y Dana Karen Medina González fueron respaldados por la SEGEY y la UADY, quienes los apoyaron desde el Concurso Estatal de la Olimpiada de Matemáticas en 2023. Su preparación incluyó entrenamientos intensivos y concentraciones en todo el país, culminando en su participación en la IMC 2024 en Lucknow, India. Este logro destaca la excelencia académica de los estudiantes y el esfuerzo conjunto de las instituciones educativas en Yucatán.
Las rarezas
de Pi, el número con más fans del mundo (que ni siquiera es un número)
Pi es una constante
matemática que ha cautivado a mentes curiosas durante siglos. Representada por la decimosexta letra del alfabeto
griego (π), Pi es la relación entre
la longitud de una circunferencia y su diámetro. Esta definición aparentemente simple encierra una complejidad sorprendente, ya que el valor de Pi
es una constante universal que se mantiene constante independientemente del tamaño de la circunferencia que estemos
considerando. Esto significa que, sin importar
si la circunferencia es tan pequeña como un átomo o tan grande como el universo observable, la relación entre
su longitud y su diámetro será siempre la misma.
Pi puede aproximarse
a través de fracciones y decimales, nunca puede ser expresado de manera exacta como la división
de dos números enteros o como la solución
de una ecuación polinómica con coeficientes enteros. Esta propiedad única de Pi lo convierte en un objeto de
estudio fascinante para matemáticos y aficionados
por igual, ya que sus infinitos decimales aparentemente no siguen ningún patrón discernible.
A lo largo de la
historia, han surgido numerosos métodos para calcular Pi con mayor precisión. Desde las aproximaciones
geométricas utilizadas por antiguos matemáticos como Arquímedes hasta los algoritmos computacionales modernos Estos cálculos han dado lugar a récords
impresionantes, como el reciente cálculo
de 63
billones de cifras.
https://www.bbc.com/mundo/articles/c84d1lzymrwo
Tres estudiantes de Yucatán fueron seleccionados para representar a México en la IMC 2024 tras su destacada participación en competencias nacionales de matemáticas. José Antonio Bernal Massa, Víctor Gerardo Vázquez Basto y Dana Karen Medina González fueron respaldados por la SEGEY y la UADY, quienes los apoyaron desde el Concurso Estatal de la Olimpiada de Matemáticas en 2023. Su preparación incluyó entrenamientos intensivos y concentraciones en todo el país, culminando en su participación en la IMC 2024 en Lucknow, India. Este logro destaca la excelencia académica de los estudiantes y el esfuerzo conjunto de las instituciones educativas en Yucatán.
Las rarezas de Pi, el número con más fans del mundo (que ni siquiera es un número)
Pi es una constante
matemática que ha cautivado a mentes curiosas durante siglos. Representada por la decimosexta letra del alfabeto
griego (π), Pi es la relación entre
la longitud de una circunferencia y su diámetro. Esta definición aparentemente simple encierra una complejidad sorprendente, ya que el valor de Pi
es una constante universal que se mantiene constante independientemente del tamaño de la circunferencia que estemos
considerando. Esto significa que, sin importar
si la circunferencia es tan pequeña como un átomo o tan grande como el universo observable, la relación entre
su longitud y su diámetro será siempre la misma.
Pi puede aproximarse
a través de fracciones y decimales, nunca puede ser expresado de manera exacta como la división
de dos números enteros o como la solución
de una ecuación polinómica con coeficientes enteros. Esta propiedad única de Pi lo convierte en un objeto de
estudio fascinante para matemáticos y aficionados
por igual, ya que sus infinitos decimales aparentemente no siguen ningún patrón discernible.
A lo largo de la
historia, han surgido numerosos métodos para calcular Pi con mayor precisión. Desde las aproximaciones
geométricas utilizadas por antiguos matemáticos como Arquímedes hasta los algoritmos computacionales modernos Estos cálculos han dado lugar a récords
impresionantes, como el reciente cálculo
de 63
billones de cifras.
https://www.bbc.com/mundo/articles/c84d1lzymrwo
Tadeo Rivera: El niño queretano «Maestro de las Matemáticas»
Tadeo Rivera Esqueda, un niño de 11 años de Querétaro, México, se ha destacado por sus habilidades matemáticas excepcionales.
Conocido como "El maestro matemático" o "El niño genio", ganó el campeonato mundial del Grand Champion Aloha Mental Arithmetic en 2023 en Malasia. Su pasión por las matemáticas surgió en tercer grado de kinder, y desde entonces ha demostrado un talento excepcional, incluso superando a niños mayores en competencias escolares. A pesar de su éxito, Tadeo no se siente presionado y prefiere disfrutar de su infancia.
Aunque algunos niños se preparan intensamente para competir, él evita el estrés y no estudia demasiado. Los profesores lo reconocieron como un niño dotado, y aunque se aburre en clase, valora la compañía de sus amigos. Se está considerando ajustar su plan de estudios para adaptarse a sus habilidades, pero sin necesariamente adelantarlo de grado.
https://lavozdequeretaro.com/cultura/tadeo-rivera-el-nino-queretano-maestro-de-las-matematicas/
“Preocupación por la caída del rendimiento académico en matemáticas, lectura y ciencia”
Un informe reciente de la OCDE, el Programa para la Evaluación Internacional de Estudiantes (PISA), ha puesto de manifiesto una preocupante disminución en el rendimiento académico de los estudiantes en matemáticas, lectura y ciencia. Este descenso en los resultados educativos es un fenómeno que se observa en diversos países del mundo, incluyendo a México. Las causas de esta problemática son complejas y multifactoriales, e incluyen aspectos como la falta de motivación del alumnado, las deficiencias en la formación del profesorado y las carencias en las infraestructuras educativas. Ante este panorama, surge la necesidad de buscar soluciones innovadoras y eficaces para abordar estos desafíos educativos. En este contexto, la tecnología se presenta como una herramienta con un gran potencial para mejorar el aprendizaje de los estudiantes. Una de las iniciativas que se plantea como clave para mejorar el rendimiento académico en matemáticas, lectura y ciencia es el uso de herramientas digitales que faciliten la resolución de ejercicios y muestren el paso a paso de la solución. Este tipo de herramientas permiten a los estudiantes aprender de forma autónoma, repitiendo los pasos de la solución y comprendiendo los conceptos matemáticos involucrados.
https://www.20minutos.es/minuteca/matematicas/1/
“Medallas en la Olimpiada Internacional de Matemáticas”
La delegación peruana ha brillado en la Olimpiada Internacional de Matemática (IMO) 2024, celebrada en [Ciudad sede de la IMO 2024], obteniendo tres medallas de plata y tres de bronce. Este logro es un motivo de gran orgullo para el país y demuestra el talento y la dedicación de los jóvenes matemáticos peruanos. Los medallistas de plata son: Sebastián Lozada Gálvez del colegio Saco Oliveros, José Rojas Carlos del colegio Saco Oliveros, Renato Gaitán García** del colegio Saco Oliveros. Los medallistas de bronce son: David Rivera López del colegio Peruano-Suizo, Jorge Luis Ysla Chávez del colegio Mayor de San Marcos y Gianfranco Huamán Torres del colegio Saco Oliveros
Este éxito es el resultado del esfuerzo conjunto de los estudiantes, sus profesores, sus familias y las instituciones que los han apoyado. El Ministerio de Educación, la Universidad Nacional Mayor de San Marcos y la Sociedad Peruana de Matemática han jugado un papel importante en la preparación de los participantes para esta competencia internacional.
https://elcomercio.pe/noticias/matematicas/
“Chileno resuelve problema matemático de casi un siglo de antigüedad”
El matemático chileno Hector Pastén ha logrado resolver un problema matemático que tenía casi un siglo de antigüedad. El problema, que se origina en los trabajos de Kurt Mahler y Sarvadaman D. S. Chowla en la década de 1930, trata sobre la estimación del tamaño del mayor factor primo de los números que son el sucesor de un cuadrado, tales como 2, 5, 10, 17, entre otros. Pastén, quien actualmente se desempeña como investigador en el Instituto Nacional de Matemática Pura y Aplicada (IMPA) de Brasil, ha desarrollado un nuevo método para abordar este problema. Su método se basa en el uso de herramientas de la teoría analítica de números y ha permitido obtener una estimación precisa del tamaño del mayor factor primo para estos números. Este logro es un hito importante en la teoría de números y representa un avance significativo en la comprensión de la distribución de los factores primos. El trabajo de Pastén ha sido publicado en la prestigiosa revista “Annals of Mathematics”.
https://www.clarin.com/internacional/resolvio-problema-matematico-siglo-antiguedad_0_pSWSWXhSfR.html
Fue la primera programadora de la historia y predijo la existencia de la inteligencia artificial
Ada Lovelace, reconocida como la primera programadora informática, destacó por sus contribuciones en el siglo XIX al reconocer el potencial de las computadoras como máquinas capaces de resolver problemas matemáticos mediante la programación. Educada en matemáticas por su madre, Lovelace se interesó por el trabajo de Charles Babbage, pionero en computación. Tradujo y complementó con sus notas el trabajo de Luigi Menabrea sobre la máquina analítica de Babbage, anticipando conceptos de algoritmos informáticos y prediciendo la existencia de la inteligencia artificial. Falleció a los 36 años, pero su legado como visionaria y pionera en la informática perdura. El segundo martes de octubre se celebra el Día de Ada Lovelace en honor a sus contribuciones a la ciencia y la tecnología, especialmente en el ámbito de la programación y las matemáticas.
https://www.nationalgeographicla.com/ciencia/2023/10/fue-la-primera-programadora-de-la-historia-y-predijo-la-existencia-de-la-inteligencia-artificial, Fue la primera programadora de la historia y predijo la existencia de la inteligencia artificial
Campeonato Escolar de Matemáticas reunió a más de 600 estudiantes
Un total de 28 establecimientos educacionales de la Región de Valparaíso participaron en el Campeonato Escolar de Matemáticas 2024, organizado por el Instituto de Matemáticas de la PUCV, con la asistencia de cerca de 600 estudiantes de enseñanza básica. Los participantes, provenientes de varias comunas, realizaron pruebas individuales y grupales con miras a futuras sesiones en mayo, junio, agosto y septiembre. El coordinador regional del evento resaltó su importancia en la educación matemática y en el desarrollo de habilidades como el trabajo en equipo y el pensamiento analítico. Los estudiantes consideraron que la actividad fue un interesante espacio de encuentro en torno a las matemáticas que los motivó a seguir aprendiendo y adquiriendo nuevos conocimientos sobre ellas. Por ejemplo, Amelia Palma, alumna de tercero medio del Colegio San Pedro Nolasco, señaló que decidió volver a competir debido a la buena experiencia que consiguió, además de la gente nueva que conoció.
https://www.adprensa.cl/cronica/campeonato-escolar-de-matematicas-reunio-a-mas-de-600-estudiantes/, Campeonato Escolar de Matemáticas reunió a más de 600 estudiantes
Lian, el pequeño genio de las matemáticas de Villaverde en Culiacán
Lian Martínez Lizarraga, un niño de 10 años de la primaria Natalio Landeros, destaca por su habilidad en matemáticas, participando en olimpiadas y obteniendo excelentes calificaciones. Desde los 5 años mostró su destreza en esta materia y siempre obtiene altas calificaciones. Aunque se considera un niño común, disfruta de su tiempo libre creando paisajes en juegos como Minecraft y desarrollando mecanismos. Sueña con ser diseñador gráfico como su mamá o programador de juegos. A pesar de ciertas dificultades para socializar, tiene muchos amigos en la escuela. Participa activamente en las olimpiadas de matemáticas y aspira a dedicarse a las ciencias en el futuro, mostrando una disposición constante para aprender y compartir su conocimiento con sus compañeros.Dice con modestia mientras baja un poco el volumen de su voz para que los niños que merodean por el lugar, no escuchen.
Lian siente orgullo por sus logros. Para él, lo más importante es seguir aprendiendo. "Lo que verdaderamente me importa es aprender más de matemáticas, no que me digan que soy muy inteligente", dice con cierta pena.
https://www.tusbuenasnoticias.com/historias/buenas-historias/descubre-a-lian-martinez-lizarraga-genio-de-las-matematicas/33045, Lian, el pequeño genio de las matemáticas de Villaverde en Culiacán
Descartes y su mosca
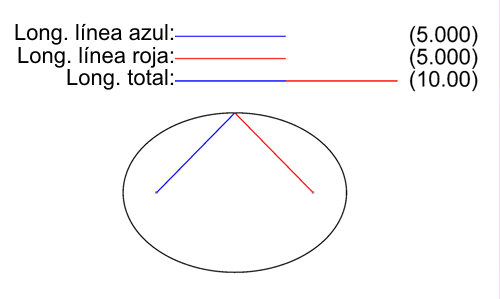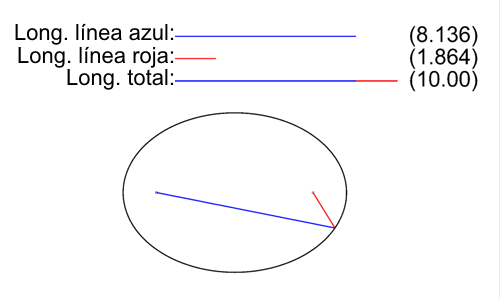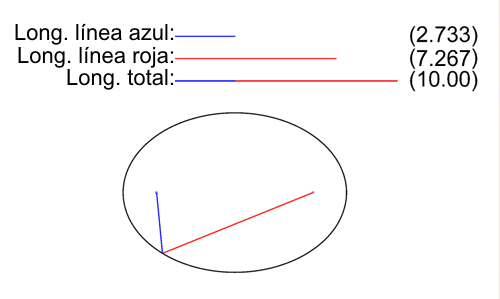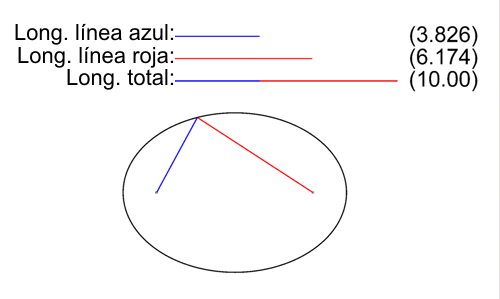
Sabemos que hay conceptos en las matemáticas que están muy relacionados a la geometría y álgebra, pero en está ocasión nos centraremos en el trabajo de Salva Fuster sobre las elipses de Steiner y las propuestas de Jakob Steiner y René Descartes.
Fuster propone que el triángulo creado por puntos medios de los lados de un triángulo original es semejante a este último, con una proporción de ½ en términos de logittttus de ¼ en términos de área. Asimismo relaciona a las áreas de las elipses e indica la unicidad de la elipse.
Jakob Steiner, matemático que rechazaba a la geometría analítica ya que para él era “impura”. Posteriormente destaca lo fundamental que es la geometría analítica, que combina a la álgebra y geometría pura, y recapitula la contribución de Descartes al crear el sistema de coordenadas cartesianas.
Descartes creó el tan conocido sistema de coordenadas cuando admiraba a una mosca y pensaba en cómo concluir su posición utilizando distancias a tres paredes. La practicidad de dicha idea da pauta a convertir líneas en ecuaciones y viceversa.
https://elpais.com/ciencia/2024-03-29/la-mosca-de-descartes.html
Cómo el ‘Machine-Learning’ puede ayudar a resolver grandes cuestiones matemáticas
Cómo el machine learning puede ayudar a
resolver grandes cuestiones matemáticas" se habla sobre cómo el
aprendizaje automático o machine learning está ayudando a los matemáticos a
resolver problemas que anteriormente se consideraban insolubles. Se menciona
cómo los algoritmos de machine learning pueden ayudar a explorar patrones y
relaciones complejas en grandes conjuntos de datos, lo que puede conducir a importantes
avances en las matemáticas.
https://www.infobae.com/america/tecno/2021/12/02/como-el-
machine-learning-puede-ayudar-a-resolver-grandes-cuestiones-
matematicas/
Ecuaciones en la multitud: las matemáticas explican los carriles espontáneos que forman los peatones para no chocar
un reciente estudio publicado en la revista Science explica el fenómeno de la formación espontánea de carriles en multitudes. Cuando las personas se mueven en dos direcciones en una multitud, inconscientemente crean carriles en cada sentido, con una anchura aproximada de dos cuerpos. Las personas se incorporan a un carril en la dirección que desean y avanzan en él, expulsando a aquellos que van en dirección opuesta. El estudio utiliza ecuaciones diferenciales para describir matemáticamente este fenómeno y se realizaron experimentos que confirmaron su validez.
Los carriles no siempre son rectos, pueden ser curvos o inclinados dependiendo de la situación. Los investigadores descubrieron que los carriles curvos tienen forma de parábola cuando se dirigen hacia una salida estrecha o forma de elipse cuando hay dos salidas. Este hallazgo es novedoso y desconocido hasta ahora.
El conocimiento de cómo se desarrolla el flujo de multitudes en espacios reducidos es crucial para prevenir avalanchas y aplastamientos. La arquitectura y el urbanismo toman en cuenta estos estudios para diseñar espacios seguros. En el caso de movimientos en más de dos direcciones, pueden surgir problemas y choques entre personas, lo que hace que los carriles desaparezcan y se pierdan los patrones de movimiento ordenado.
Este tipo de investigaciones también se aplican al estudio de situaciones reales, como las estampidas en peregrinaciones o eventos masivos, con el objetivo de entender cómo lograr que la formación espontánea de carriles en una multitud sea segura y evitar tragedias como avalanchas.
Toro, V., Toro, V., & Nasser, F. A. (2023,
May 9). Ecuaciones en la multitud: las matemáticas explican los carriles
espontáneos que forman los peatones para no chocar. El País. https://elpais.com/ciencia/2023-05-09/ecuaciones-en-la-multitud-las-matematicas-explican-los-carriles-espontaneos-que-forman-los-peatones-para-no-chocar.html
Las matemáticas: el ingrediente secreto de Pablo Picasso en el surgimiento del cubismo
La creación del cubismo por parte de Pablo Picasso fue una revolución en el mundo del arte en los comienzos del siglo XX. Esta revolución en el arte tuvo un ingrediente inesperado: las matemáticas, en una época marcada por grandes descubrimientos científicos y un gran interés de la sociedad por estos avances. Mercedes Siles, catedrática de Álgebra de la Universidad de Málaga, comenzó a investigar sobre la relación entre las matemáticas y el arte de Picasso hace ocho años después de visitar en el Museo Picasso de Málaga la exposición Movimientos y secuencias. La catedrática de Álgebra afirma que la belleza, las matemáticas y el arte caminan siempre paralelas, y que el cubismo de Picasso intentaba reflejar la cuarta dimensión que apareció con la Teoría de la Relatividad, inspirándose en la obra de Durero, quien también utilizó cubos para matematizar el arte en el Renacimiento. La influencia de la ciencia en la sociedad de la época y en el grupo de amigos de Picasso, que se reunían en el Bateau-Lavoir de París, también fue una fuente de inspiración para el artista. Según Siles, aunque Picasso nunca dijo que las matemáticas influyeran en su obra, es probable que fuera consciente de esa influencia matemática, ya que la ciencia permeaba entonces la sociedad.
Efe, J. L. P. /. (2023, April 14). Las
matemáticas: el ingrediente secreto de Pablo Picasso en el surgimiento
del cubismo. www.20minutos.es - Últimas Noticias. https://www.20minutos.es/noticia/5118796/0/las-matematicas-el-ingrediente-secreto-de-pablo-picasso-en-el-surgimiento-del-cubismo/
Un estudiante español explica cómo son los exámenes de Matemáticas en Estados Unidos: «Más facilitos»
Un
estudiante español que estudia en Ohio publicó un video de TikTok que compara
clases y exámenes de matemáticas en España y Estados Unidos. El usuario
@yago.rdgzz asegura que las clases de matemáticas en Estados Unidos son más
fáciles y menos estructuradas que las de España. Explica que las clases se
hacen sin libros y que las notas se envían al profesor después de la lección. Los
exámenes también son fáciles, solo requieren las notas enviadas por el
profesor, y los problemas son los mismos, pero con diferentes ejemplos. El
usuario también comparte algunos ejercicios de examen y afirma que el primer
año de secundaria en Estados Unidos es más fácil que en España. El video ha
obtenido más de 1 millón de visitas y ha provocado un debate entre los usuarios
sobre las diferencias en los sistemas educativos entre los dos países. Algunos
han criticado el sistema estadounidense por ser demasiado fácil, mientras que
otros lo han defendido por proporcionar un aprendizaje más práctico y práctico.
M,
J. (2023, April 18). Un estudiante español explica cómo son los exámenes de
Matemáticas en Estados Unidos: «Más facilitos». Abc. https://www.abc.es/recreo/estudiante-espanol-explica-examenes-matematicas-estados-unidos-20230417214353-nt.html
Infinito, la fuente de paradojas matemáticas
Comienza
el texto con una advertencia “La locura del infinito es un estado del alma que,
una vez que te hechiza, nunca te abandonará”. Al empezar, la tortuga parte de
cierta ventaja; al paso del tiempo, cuando Aquiles ha alcanzado el punto
inicial de la tortuga, esta se ha movido un poco, así que sigue por delante. El
primero en pensar en estos términos fue Arquímedes, que propuso el llamado
método de exhausción para calcular el área encerrada en una parábola, el área
de la esfera y también para aproximar el número Pi y que es predecesora del
cálculo diferencial, propuesto por Newton y Leibniz siglos después.. El libro
de Prado-Bassas concluye con un capítulo dedicado al concepto de biyección: una
herramienta matemática que permite establecer una correlación entre dos
conjuntos y, así, compararlos. El matemático Georg Cantor la usó para
clasificar los conjuntos infinitos, ya que, como demostró, existían en
diferentes tamaños.
“Mexicanas, segundo lugar de Iberoamérica en la olimpiada europea de matemáticas
Con este resultado México suma dos preseas más a su récord en la historia
de sus participaciones en esta competencia, en la que ha ganado hasta la fecha cinco oros, 14 platas
y 15 bronces.
La EGMO tiene el objetivo de romper los estereotipos de género, sobre todo para desechar el prejuicio de que las mujeres no son tan buenas como los hombres para las matemáticas y las ciencias exactas.
Las estudiantes que integraron la delegación nacional, entrenadas y seleccionadas por la Olimpiada Mexicana de Matemáticas (OMM), son Rosa Victoria Cantú Rodríguez, Andrea Escalona
Contreras, Andrea Sarahí Cascante
Duarte, Ana Camila
Cuevas González.
Con este resultado, dicen los entrenadores de la OMM, “se demuestra que en México hay talento para las matemáticas”.
En el puntaje por países el equipo femenino ocupó el lugar 29 de 55 participantes de todo el mundo.
Su presencia en la EGMO ha motivado a que más chicas se interesen en inscribirse en las competencias de matemáticas nacionales y que muchas lleguen a niveles
más altos, concluyan los organizadores de la OMM.
Referencia : https://www.jornada.com.mx/notas/2023/04/19/ciencia-y-tecnologia/mexicanas-segundo-lugar-de-iberoamerica-en-olimpiada-europea-de-matematicas/ _
El extraordinario concepto sobre la nada que llevó a la invención del 0”
Cuentan que un día hace casi 2.300 años, Alejandro Magno, tras conquistar Persia, llegó a orillas del río Indo y encontró lo que llamó un gimnosofista, o sea, un sabio desnudo, sentado en una roca mirando al cielo.
"¿Qué estás haciendo?" preguntó Alejandro.
"Experimentando la nada. Y tú, ¿qué estás haciendo?", respondió el gimnosofista.
Ambos rieron, cada uno pensando que el otro era un tonto y estaba desperdiciando su vida.
Ese es un relato que narra el renombrado mitologista Devdutt Pattanaik para ilustrar las diferencias entre la cultura occidental y la india.
Pero nos habla también de cuán filosóficamente abiertos estaban en India al concepto de la nada mucho antes de que se escribiera el primer 0.
https://www.bbc.com/mundo/noticias-65033379_ _
“No me gusta que me llamen mujer matemática. Soy una persona matematica que resulta ser mujer”
Uhlenbeck ha revolucionado la ciencia en la encrucijada entre la física y las matemáticas. Sus ideas vanguardistas se han aplicado en campos como la teoría de cuerdas y la geometría del espacio-tiempo. Y todo lo ha logrado en un mundo, el de las matemáticas, “maravilloso y divertido”, pero que estuvo prácticamente vetado a las mujeres hasta que llegó ella. Cuando comenzó a buscar trabajo hace medio siglo, le espetó que nadie contrataba a chicas matemáticas, porque debería estar en casa y tener bebés.
Fuente: https://elpais.com/elpais/2019/03/22/ciencia/1553282571_242902.html
Una mujer gana por primera vez el 'Nobel' de matemáticas
Por qué crees que has visto una película entera pero en realidad te has perdido la mitad
Como es bien sabido, la circunferencia es una curva cerrada cuyos puntos equidistan de otro, que es el centro. Y en el caso de la elipse, es la suma de distancias a otros dos puntos, llamados focos, lo que permanece constante para todos los puntos de la curva.
La fórmula de la elipse es x2/a2 + y2/b2= 1. Si a = b, la fórmula se convierte en x2 + y2 = a2, y la elipse, en una circunferencia de radio a. Y del mismo modo que la circunferencia se puede considerar un caso particular de la elipse, podemos considerar que la elipse es un caso particular de una familia de curvas de la forma xn/an + yn/bn = 1. De hecho, así lo consideró el matemático francés Gabriel Lamé, que dio nombre a estas curvas (también llamadas superelipses) y las estudió a mediados del siglo XIX.
Cien años después, el escritor e ingeniero danés Piet Hein, el inventor del Hex, estudió una curva de Lamé en particular: la de exponente n = 2.5, con a = 4 y b = 3, y la aplicó al diseño de mesas y otros muebles, así como al trazado de una rotonda en una plaza rectangular de Estocolmo. La elipse convencional parecería la primera opción, por una sencilla regla de tres: circunferencia es a cuadrado como elipse a rectángulo. ¿Qué ventaja tiene la superelipse de Hein sobre la elipse? ¿Qué ocurre a medida que aumenta el exponente n?
Haciendo girar su superelipse alrededor de su eje mayor, Hein obtuvo un interesante superelipsoide, denominado “superhuevo”, que ha sido reproducido a muy distintos tamaños, como objeto de regalo y como escultura, y que posee una sorprendente propiedad que no comparte con su primo el elipsoide de revolución. ¿Cuál?
https://elpais.com/elpais/2019/02/14/ciencia/1550139185_074756.html
Las matemáticas que descifraron la máquina
«Enigma» de los nazis
Es bien conocida la participación fundamental de Alan Turing y su equipo
para descifrar los mensajes que los alemanes mandaban encriptados con la
máquina «Enigma», y que tanto contribuyó a acortar la II Guerra Mundial y a
asegurar el triunfo aliado. Son menos conocidas las importantes aportaciones de distintos matemáticos polacos, con
Marian Rejewski a la cabeza, así como las matemáticas que
hay debajo de la compleja tarea que realizaron. Desvelaremos en este artículo
ambos aspectos y veremos que es un asunto de plena actualidad: tiene algo en
común con el cifrado que se usa en WhatsApp.
Las matemáticas que descifraron la máquina «Enigma» de los nazis
Niños aborígenes australianos capaces de contar sin
números
Según un nuevo estudio sobre niños aborígenes
australianos realizado por el University College de Londres y la Universidad de
Melbourne, conocer las palabras para designar los números no es necesario para
poder contar. En el estudio se examinó a ciertas poblaciones indígenas
australianas que tienen vocabularios muy limitados para los números, trabajando
con niños de edades comprendidas entre los cuatro y los siete años, de dos
comunidades indígenas con difierente idioma. En ambas lenguas, existen palabras
para uno, dos, algunos y muchos. Y tampoco parece haber ningún gesto para los
números.En el estudio, se comprobó que esa carencia de palabras o gestos para
los números en los niños examinados no les impide realizar una serie de tareas
relacionadas con ellos.Los resultados de este nuevo estudio sugieren, por
tanto, que los seres humanos poseemos un mecanismo innato para contar, que
puede desarrollarse de forma diferente en los niños con discalculia, y que la
falta de un vocabulario para los números no debe impedirnos realizar tareas
numéricas que no requieran de palabras para designar los números. Este sistema
innato para contar nos permite reconocer y representar el número de objetos de
un conjunto.
Ser bueno en geometría “es innato”
Según los científicos del College de France y la
Universidad de Harvard, la comprensión de nociones básicas de geometría puede
ser el resultado de una habilidad innata, y no del aprendizaje. Los científicos
llegaron a esta conclusión después de comparar los resultados de pruebas
realizadas a niños estadounidenses y niños de la tribu amazónica Munduruku, que
vive en un lugar aislado de la civilización. Los niños Munduruku obtuvieron los
mismos resultados que sus contemporáneos en Estados Unidos. “La comprensión
espontánea de conceptos geométricos y mapas demostrado por esta remota
comunidad humana es evidencia de que el conocimiento geométrico básico es un
constituyente universal de la mente humana”, explica Elizabeth Spelke, una de
las autoras del estudio.
Las matemáticas celestes son equivalentes a las de
la física atómica
Un equipo de científicos norteamericanos, formado
por un ingeniero, un físico y un matemáticohan descubierto un paralelismo
inesperado entre las matemáticas de la mecánica celeste y las de la física
atómica, Atomolo que constituye un descubrimiento de gran interés teórico y una
importante contribución para la concepción de las misiones espaciales o el
desarrollo de la química. Las ecuaciones matemáticas que describen el
movimiento de los cuerpos celestes son las mismas que describen los niveles
energéticos de los electrones en los sistemas simples, aunque a nivel molecular
se piensa que también pueden ser aplicadas. La descripción matemática de
fenómenos físicos de escalas tan diferentes, astronómica, atómica o molecular,
es la misma, lo que constituye un descubrimiento de gran interés teórico y una
importante contribución para la concepción de las misiones espaciales o el
desarrollo de la química, toda vez que la dinámica de una escala puede
aplicarse a la otra.
Complicarse la vida
Algunos lectores, dando por supuesto que el haba y la figurita no podían estar en el mismo trozo de roscón, han hallado una probabilidad ligeramente mayor de tener que pagarlo (23,33%). Es una suposición razonable, pues en la práctica el pastelero nunca pondría ambas “sorpresas” tan juntas como para que pudieran coincidir en un mismo trozo de 100 g; pero el enunciado no excluye esa posibilidad: el de las sorpresas del roscón es uno de esos problemas en los que, sin darnos cuenta, nos autoimponemos más condiciones de las que se nos piden (con lo que parecen poner de manifiesto una paradójica tendencia a “complicarse la vida” más de lo necesario).
https://elpais.com/elpais/2018/04/17/ciencia/1523964928_127889.html
Aubrey de Grey descifra el problema de Hadwiger-Nelson
Aubrey de Grey es un famoso biogerontólogo inglés trabaja en una técnica de recuperación de tejidos con la que asegura que podremos vivir más de mil años. Pero también es un enamorado de las matemáticas, dedica parte de su tiempo a intentar solucionar misterios y lo ha conseguido con el problema de Hadwiger-Nelson.
Consiste en averiguar el menor número de colores necesarios para colorear todos los puntos en un gráfico, sin que existan dos puntos conectados que sean del mismo color. Desde los años 50, los matemáticos han reducido las posibilidades a cuatro, cinco, seis o siete pero ahora, De Gray ha encontrado que el número mínimo cromático es cinco.
La solución matemática más larga de la Historia
Por qué los números primos siguen fascinando a
los matemáticos, 2.300 años después
Los algoritmos permiten obtener nuevas
cifras de π
El número Pi sigue encerrando misterios que los matemáticos de todo el mundo tratan de resolver. Por ejemplo, todavía no se sabe si es un número normal en base 10, es decir si contiene en su desarrollo decimal cualquier sucesión finita de dígitos con la frecuencia que sugiere su tamaño. Una manera de investigar esta característica es hacer estudios estadísticos en los millones de cifras decimales conocidas del número. Para ello, es necesario computar una cantidad cada vez mayor de dígitos de Pi.Esto se consigue gracias a los algoritmos que idean los matemáticos en base a las fórmulas de la teoría de números en las que aparece Pi. Los más empleados son los algoritmos iterativos y las series.
Así aprenden los niños las matemáticas
Niña aprendiendo matemáticas
Durante la etapa de la escolarización, hay un momento crucial en que los niños dejan de utilizar los dedos y empiezan a hacer las cuentas de cabeza. ¿Qué pasa en nuestro cerebro para adquirir esta habilidad? ¿Cómo se forma una mente matemática? Esto es lo que se han preguntado neurocientíficos de la Escuela de Medicina de la Universidad de Stanford, que han realizado resonancias magnéticas a niños, adolescentes y adultos mientras resolvían problemas aritméticos. Los expertos comprobaron que en los niños mayores se activaba más el área del hipocampo, vinculada a los recuerdos, y menos la corteza prefrontal y parietal, zonas neuronales relacionadas con el acto de contar. Es decir, al cumplir años recurrimos cada vez más a la memoria para las matemáticas. Sin embargo, en el caso de los adolescentes y adultos, funcionaba a pleno rendimiento el neocórtex, donde se asienta la información archivada a lo largo de la vida en el cerebro maduro. Según Vinod Menon, principal investigador del estudio, “esto significa que el hipocampo proporciona durante la infancia una especie de andamio para aprender y consolidar los datos en la memoria a largo plazo”. Los científicos esperan que las conclusiones de su investigación sirvan para paliar la dificultad innata de algunos alumnos con las temidas “mates”.
http://www.muyinteresante.es/ciencia/articulo/asi-aprenden-los-ninos-las-matematicas-471408442448
La genética marca el rendimiento en matemáticas
Resultado de imagen para gif de genetica
Esta ardua asignatura para muchos podría tener una estrecha relación con determinados factores genéticos, según ha confirmado una reciente investigación de la Universidad de Granada. Tal y como explican en el estudio, publicado en la revista Learning and Individual Difference, existe una estrecha relación entre el rendimiento en matemáticas y la exposición a la testosterona del feto durante el embarazo. En la investigación participaron 516 estudiantes del primer curso de la facultad de Empresariales de la Universidad de Granada, y para calcular la exposición de cada uno de ellos a la testosterona durante su desarrollo fetal, se recurrió a la medición del llamado ‘digit radio’, un parámetro que mide el ratio entre el dedo índice y el dedo anular. Según este parámetro, aquellos que tuvieron una carga más alta de testosterona en el vientre materno presentan un dedo anular más largo. En general, los niños reciben una dosis más alta que las niñas, por lo que el ‘digit radio’ es menor en los varones. Los resultados del estudio revelaron que unos niveles intermedios del ‘digit radio’ se asocian a buenos resultados en esta disciplina, mientras que por el contrario, tanto los ‘digit radio’ altos como bajos, mostraban peores resultados. Además, la relación entre este biomarcador y las calificaciones de la asignatura no presentaban diferencias entre hombres y mujeres, lo que implica que el género no influye para nada. Para afianzar esta teoría, la autora principal del trabajo y directora del departamento de Economía aplicada de la universidad, Ángeles Sánchez-Domínguez, explica que esta pauta no se ha encontrado en otras asignaturas, tan solo en matemáticas, lo que supone que existe una relación cuadrática entre dicha disciplina y el ‘digit radio’, independientemente de si el alumno lleva un expediente alto o bajo en el resto de materias.
http://www.muyinteresante.es/ciencia/articulo/la-genetica-marca-el-rendimiento-en-matematicas-351421673556
Matemáticas, la solución para predecir el punto óptimo de curación del jamón
Jamón
Hasta ahora, el método para fijar el cambio de periodo en el proceso de producción consistía solamente en la percepción de los expertos de cada industria, obtenida a través de su larga experiencia. Investigadores del Instituto de la Grasa (CSIC-Sevilla) han querido dar un paso más y han desarrollado ecuaciones matemáticas para hacer un seguimiento más preciso del comportamiento de las piezas, con el objetivo de saber cuándo es el mejor momento de que, por ejemplo, pasen del secadero a la maduración en bodega. Según han señalado los investigadores, el modelo matemático consiste en analizar parámetros como el perfil de la grasa y la pérdida de humedad. Para obtenerlo, monitorizaron diez jamones durante el proceso de curación a través de tres años. El responsable del estudio, Manuel León, del Instituto de la Grasa, explica que se obtenían datos cada hora, “lo que convertía a este seguimiento en el primero que se realiza en jamones durante tanto tiempo y sin degradar el producto”. Tras analizar los datos, estudiaron cómo evoluciona la fracción de lípidos del tejido adiposo subcutáneo del jamón ibérico durante el proceso de curado en seco. Además, determinaron la generación de los llamados compuestos volátiles, responsables de los aromas del producto, y que los expertos agruparon por familias. Así, comprobaron los cambios en las cantidades de estos compuestos en la grasa subcutánea durante el proceso de maduración. Esto les hizo determinar que “un aumento de la temperatura está relacionado con la generación y pérdida de los hidrocarburos y que, durante la curación, se redujo su cantidad”, concretan los expertos. Pero, ¿hasta qué punto podrían optimizar estos nuevos modelos los procesos de la industria cárnica? En opinión de León, “si se conoce todo el recorrido de la pieza es más fácil localizar dónde se ha producido algún fallo, lo que beneficia a la trazabilidad y a la seguridad alimentaria”.
http://www.muyinteresante.es/ciencia/articulo/matematicas-la-solucion-para-predecir-el-punto-optimo-de-curacion-del-jamon-231437554389
Un 60% de los estudiantes sufre 'ansiedad matemática'
Resultado de imagen para gif de estresarse
Si intentar resolver un problema matemático te provoca tensión, preocupación, inquietud, irritabilidad, impaciencia, confusión, miedo y bloqueo mental, no hay duda de que eres víctima de la "ansiedad matemática" o miedo extremo a esta asignatura.
Este mal es bastante común, según revela un nuevo estudio realizado por expertos en Didáctica de la Matemática y Psicología Evolutiva de la Universidad de Granada publicado en la revista Investigación en Educación Matemática. Tras aplicar a 885 estudiantes de primer curso la Escala de Ansiedad Matemática de Fennema-Sherman, un cuestionario validado por expertos de todo el mundo que se utiliza desde los años 70, los investigadores han llegado a la conclusión de que 6 de cada 10 estudiantes universitarios sufre ansiedad matemática. Ésta podría definirse como "el pánico, indefensión, parálisis y desorganización mental que surge cuando a un sujeto se le exige resolver un problema matemático".
Según concluyen los investigadores, un efecto indirecto de este tipo de ansiedad es que pueden condicionar negativamente el tipo de carrera que eligen los estudiantes españoles. Dicho de otro modo, muchos universitarios eligen carreras distintas a las que realmente querrían para evitar cursar asignaturas relacionadas con las matemáticas.
http://www.muyinteresante.es/salud/articulo/un-60-de-los-estudiantes-sufre-ansiedad-matematica
En busca de las ecuaciones de la política
mates2
Un equipo de expertos de la Universidad Politécnica de Valencia (UPV) está desarrollando un trabajo de investigación para definir modelos matemáticos basados en ecuaciones diferenciales que permitan predecir cómo evolucionarán las ideologías y tendencias de pensamiento en la sociedad.
Según Rafael Villanueva, investigador del Instituto de Matemáticas Multidisciplinar de la UPV, las ecuaciones diferenciales pueden ayudar a averiguar, por ejemplo, ?qué posibilidades existen de que una persona que tiene una ideología determinada, cambie su forma de pensar y se encamine hacia otros posicionamientos, incluso radicales o a determinados comportamientos fanáticos",
Cada una de las ecuaciones desarrolladas por Villanueva y sus colaboradores engloba una serie de parámetros que influyen en la evolución de la ideología de grupos sociales y que contemplan aspectos como la publicidad, la propaganda, la repercusión mediática, el liderazgo de un tipo de mensaje, etc. ?Estudiando los cambios en los valores de los parámetros podemos predecir los diversos escenarios ideológicos de una sociedad en un futuro cercano", afirma el investigador.
http://www.muyinteresante.es/ciencia/articulo/en-busca-de-las-ecuaciones-de-la-politica
Entrenar con un ábaco puede cambiar tu cerebro
Resultado de imagen para gif de abaco
La cuestión de la plasticidad cerebral está de moda en el ámbito de la investigación científica. El objetivo de muchos trabajos es averiguar cómo se modifica nuestro cerebro cuando lo entrenamos a través de determinadas actividades o tareas. Estos cambios pueden referirse tanto a la estructura cerebral como a la forma habitual de funcionar de las diversas áreas del cerebro. Uno de los trabajos recientemente publicado en la revista Neural Plasticity (2016) revisa los hallazgos más relevantes en cuanto a los efectos neurales que puede tener practicar con el ábaco. El ábaco es un sistema de cálculo tradicional que se usa desde hace cientos de años y a través del cual podemos ejecutar operaciones aritméticas como sumas, restas, multiplicaciones, divisiones e incluso raíces. En algunos países su uso está más extendido entre la población y en otros está encontrando adeptos. Pero, ¿tiene algún efecto sobre nuestro cerebro el uso continuado del ábaco? Yongxin Li, del Southern Medical University en China, y sus colaboradores repasan en su artículo los conocimientos que se han adquirido hasta el momento sobre este asunto. Entre los hallazgos más relevantes encontramos que:
Los estudios que se llevaron a cabo utilizando diferentes actividades y test cognitivos mostraron que el grupo de personas con más experiencia en el cálculo con ábaco activaban más su hemisferio derecho en tareas de cálculo mental, mientras que el grupo de participantes sin experiencia con el ábaco utilizaba más el lado izquierdo del cerebro. Años más tarde, otros estudios con técnicas de resonancia magnética cerebral corroboraron estos datos. De forma interesante, entrenar con el ábaco parece que produjo un efecto en otras funciones cognitivas como la inteligencia general y la memoria, lo que se conoce como 'transferencia'. Usando técnicas de imagen como la tomografía por emisión de positrones se observa que, cuando se les pone ante una tarea de cálculo mental, el cerebro de personas con gran manejo del ábaco activa de forma importante la red visoespacial en la que participan áreas fronto-parietales del cerebro. Sin embargo, cuando se trata de los no expertos en ábaco, se activan otras áreas diferentes, como el área de Broca, implicada en la memoria de trabajo verbal. Por último y más recientemente, otros estudios han hallado que el entrenamiento con el ábaco produce en los niños cambios tanto en la sustancia gris del giro frontal izquierdo, como en la sustancia blanca cerebral, que parece conservar una mejor integridad en el grupo de entrenamiento. Sigue resultando asombroso que practicar habitualmente una sola tarea como el ábaco produzca tantos cambios a nivel cerebral y de rendimiento en test. Sería interesante averiguar si entrenar diferentes funciones cognitivas puede resultar incluso más eficaz en este sentido. La ciencia hace progresos lentos sobre estas cuestiones, pero quizá no sea mala idea ir ejercitando nuestras capacidades mentales y fomentar así la plasticidad cerebral de la que disponemos.
http://www.muyinteresante.es/salud/articulo/entrenar-con-un-abaco-puede-cambiar-tu-cerebro-401475665787
¿Por qué no existe el premio Nobel de matemáticas?
¿Por qué no existe el premio Nobel de matemáticas?
Las malas lenguas cuentan que la mujer de Alfred Nobel le fue infiel con un matemático, y que por esa razón decidió ignorar a esa disciplina en sus famosos premios. Es una razón más que entendible para dejar sin galardón a los cerebritos de las mates, pero nunca se llegó a confirmar. La clave suele estar en lo más simple, y dejando a un lado temas amorosos, lo más lógico es que a Nobel no le interesaran nada las matemáticas, y esto sí que está comprobado. Nobel fue ingeniero químico, inventó la dinamita, fabricó armas y también tuvo una faceta de empresario, lo que le llevó a amasar una gran fortuna gracias a sus muchas patentes (registró 350). Los únicos números que le importaron en su vida fueron los del dinero. Con su inmensa fortuna dejó la orden en su testamento de premiar a las personas que más hubieran contribuido el año anterior a ciertas disciplinas, las más afines a sus intereses, y entre ellos, no se encontraban las matemáticas. Cada año se otorga este premio para las categorías de física, química, medicina, economía, literatura y paz. A los galardonados los elige un selecto comité formado por personalidades y organizaciones de prestigio, que tras realizar una exclusiva criba entre cientos de candidatos propuestos también por diferentes organizaciones, deciden quienes son los que más han contribuido el año anterior en cada área. Desde 1901 se llevan otorgando estos galardones, pero los matemáticos no trabajan sin reconocimiento, de eso se encargó John C. Fields. El canadiense puso el dinero para que esta disciplina obtuviera su merecido prestigio. Esta tarea la empezó en 1936 otorgando dos medallas, que posteriormente pasaron a ser cuatro. Se entregan cada cuatro años de forma que coincidan con los congresos internacionales de matemáticas, dónde se da a conocer el nombre de los afortunados. El único requisito que deben de tener estos genios aspirantes al premio es ser menor de 40 años a día 1 de enero del año del congreso. Quién decide en este caso quienes son los merecedores del premio es la Unión Internacional de Matemáticas.
http://www.muyinteresante.es/curiosidades/preguntas-respuestas/por-que-no-existe-el-premio-nobel-de-matematicas-791408531464-3
Matemáticas para predecir ataques terroristas
11s
Pedro Pinto y sus colegas de la Escuela politécnica federal de Lausana (Suiza) han desarrollado un algoritmo que permite desde detectar el origen de ataques terroristas hasta trazar la propagación de epidemias. Las simulaciones por ordenador de las conversaciones telefónicas mantenidas durante los ataques terroristas del 11 de septiembre de 2001 ha servido para ponerlo a prueba, según relatan en la revista Physical Review Letters. Según Plinio, "al reconstruir el intercambio de mensajes durante el atentado, nuestro sistema obtuvo los nombres de tres posibles sospechosos, uno de los cuales resultó ser el autor intelectual de los ataques, según la investigación oficial". El algoritmo también se puede emplear para encontrar la fuente primaria de una enfermedad infecciosa, como el cólera. En ese caso, los investigadores usaron la modelización de redes fluviales y redes de transporte humano para hallar el lugar donde aparecieron los primeros casos de infección. El método también sería útil para responder a ataques terroristas, como el ataque con gas sarín en 1995, en el metro de Tokio, en el que el gas venenoso en los túneles subterráneos de la ciudad mató a 13 personas, e hirió a cerca de 1.000. "Nuestro algoritmo no necesitaría detectores en todas las estaciones, ya que una muestra sería suficiente para identificar rápidamente el origen del ataque", señala Pinto. Además, con este método se puede encontrar la fuente de todo tipo de rumores que circulan en una red, con un número limitado de miembros de dicha red. Así, suponiendo que alguien encuentra un rumor acerca de sí mismo, que se ha propagado en Facebook, y que se ha enviado a 500 personas, a sus amigos o, incluso, a amigos de sus amigos, se podría encontrar a la persona que inició el rumor. Este método también puede utilizarse para identificar el origen de un mensaje de spam, o de un virus de ordenador, utilizando solo un número limitado de sensores dentro de la red.
http://www.muyinteresante.es/ciencia/articulo/matematicas-para-predecir-ataques-terroristas
El número más grande jamás citado
El número más grande jamás citado
Piensa un número grande, muy grande, el número (con algún nombre o significado) más grande del que hayas visto, leído u oído algo. Quizás te haya venido a la cabeza un billón, que es un 1 seguido de 12 ceros. Sí, es grande, pero seguro que también has escuchado a alguien nombrar al trillón, que es un millón de billones (formado entonces por un 1 seguido de 18 ceros) y que, por tanto, es mayor que un billón. Pero seguro que muchos habréis pensado en otros más grandes, como el googol (o gúgol). Este número está formado por un 1 seguido de 100 ceros y, según parece, inspira el nombre del buscador más famoso de internet (ya hemos comentado por aquí que los chicos de Google son bastante frikis). Sí, este número es muy grande, mucho mayor que el número de átomos del Universo conocido, 1080. Pero en realidad solamente tiene 101 cifras, por lo que es sencillo de expresar con la notación de exponentes habitual: 10100. Antes de seguir, es interesante aclarar que en este artículo hablamos de números naturales conocidos. Está claro que los números naturales son infinitos, por lo que, en teoría, podríamos escribir un número todo lo grande que quisiéramos, y después de escrito podríamos escribir otro mayor sumándole 1, multiplicándolo por 7 o elevándolo al cuadrado. La intención de este artículo es hablar de números de los cuales conozcamos su descripción y que tengan cierta relevancia dentro de las matemáticas. Aclarado esto, volvamos a los números. Los conocemos mucho más grandes que el googol, y en este blog hemos hablado de ellos: algunos primos de Mersenne. Concretamente, el más grande que conocemos tiene más de 22 millones de dígitos. Como decíamos en ese artículo, un número descomunal. El problema es complicado de entender, y más aún de resolver, pero en este artículo no nos interesa profundizar en él. La cuestión es que Ronald Graham y Bruce Rothschild demostraron que el problema tenía solución, y dieron una cota de la misma. Más adelante, en un artículo no publicado, Graham rectificó esa cota al alza, que a partir de ahí (gracias también a que Martin Gardner habló sobre ella en su famosa columna en Scientific American) se comenzó a llamar número de Graham. Como comentábamos unos párrafos más arriba, la notación que usamos habitualmente para describir número naturales se nos queda corta, por lo que necesitamos una nueva forma de escribir números. Esta nueva operación se denomina notación flecha de Knuth, en honor a su inventor, Donald Knuth. Veamos en qué consiste. Todos sabemos que cuando escribimos 43 lo que hacemos es abreviar la operación 4 · 4 · 4. Es decir, multiplicamos la base, 4, el número de veces que dice el exponente, 3. Bien, pues vamos a cambiar la forma de escribir esa operación: ahora es 4↑3. Comencemos a generalizar. Si con una flecha multiplicamos la base el número de veces que diga el exponente, ¿cómo definiríamos la operación que quedaría al poner dos flechas? Pues muy sencillo: dos flechas implican operar “flecha” el número de la izquierda la cantidad de veces que indique el número de la derecha.
http://elpais.com/elpais/2017/05/17/el_aleph/1495036614_478342.html
Un modelo matemático predice cómo
se propagan las alteraciones de un
sistema
Supongamos que un individuo ingiere un medicamento y, horas más tarde, un análisis de sangre revela que la concentración de algunos metabolitos ha cambiado respecto a lo que sería habitual. Ante esta situación, el médico intenta interpretar la cadena de acontecimientos que traen estos cambios, pero se enfrenta a desafíos significativos. En primer lugar, hay miles de metabolitos y miles de reacciones bioquímicas que transforman unos metabolitos en otros. Por otra parte, la estructura de la red metabólica se mantiene, pero las concentraciones de metabolitos han mutado por efecto de estas reacciones. En tercer lugar, el médico ignora el estado de la mayoría de los metabolitos, puesto que solo una parte de ellos, cerca del 10 %, se mide en un análisis de sangre. Con los datos que tiene a su alcance, no puede responder a preguntas como qué reacciones han provocado que la modificación metabólica se haya extendido, o cuántos metabolitos, que no se pueden medir, se han visto afectados. Investigadores del grupo de investigación SEES:lab, del Departamento de Ingeniería Química de la URV, junto con investigadores de la Unidad de Investigación Biomédica del Departamento de Medicina y Cirugía, en España, han hecho frente a ese desafío y han comprobado los resultados en casos reales, con voluntarios que ingirieron un extracto de una planta para poner a prueba el resultado de un nuevo modelo matemático que han desarrollado. Se trata de analizar un volumen muy elevado de información, buscar las conexiones entre los nodos y, finalmente, darles más o menos relevancia. Todo ello lo han aplicado a problemas dinámicos para poder saber por dónde se ha propagado en una red compleja una perturbación causada por factores externos. En definitiva, conocer una parte para poder prever el todo.
http://noticiasdelaciencia.com/not/21616/un-modelo-matematico-predice-como-se-propagan-las-alteraciones-de-un-sistema/
Matemáticas para esquivar los atascos de tráfico
Resultado de imagen para gif de trafico
Los atascos de tráfico, más allá de un quebradero de cabeza para los automovilistas, tienen un importante impacto social, económico y medioambiental. Ahora un equipo de investigadores de la Universidad Politécnica de Madrid (UPM), en España, ha desarrollado un algoritmo de toma de decisión que puede aplicarse a sistemas inteligentes de transporte para reducir las retenciones en las carreteras. El algoritmo propuesto, cuya eficiencia ha sido validada en simulaciones, recomienda a los conductores el mejor itinerario en virtud de los datos de tráfico que proporciona la red de sensores desplegados en las principales vías de circulación. El equipo de la UPM, perteneciente al Centro de Investigación en Tecnologías de Software y Sistemas Multimedia para la Sostenibilidad (CITSEM), se ha enfrentado a dos retos importantes para asegurar que la toma de decisiones sea fiable. Por un lado, la incertidumbre relacionada con los datos recibidos de los sensores, ya que la información puede ser incompleta, presentar inconsistencias o haber perdido precisión durante su medición, procesado y visualización. Por otro, la información del contexto obtenida por los sensores es variable, lo que obliga a que el algoritmo sea capaz de ajustar la toma de decisiones a esos cambios. Los investigadores han adaptado para su trabajo uno de los algoritmos de toma de decisiones más utilizados, denominado Proceso Analítico Jerárquico -en inglés, Analytic Hierarchy Process (AHP)- , con el fin de emplearlo en los sistemas inteligentes de transporte teniendo en cuenta los retos antes mencionados. Para ello, han fusionado dos variantes de ese algoritmo: FAHP y DAHP. En la primera, se utiliza la lógica difusa para realizar los cálculos atendiendo al efecto de la incertidumbre en los datos recibidos; en la segunda, las variables utilizadas en los cálculos se consideran dinámicas y, por tanto, variables con el tiempo.Zheng, que no tenía novia desde hace años, optó por fabricarse su propia esposa después de que su familia y amigos llevaran tiempo presionándole para que se casara, según contó a la prensa. Yingying es capaz de hablar mediante una conexión a un ordenador con textos y archivos de audio almacenados, también puede reconocer fotografías y objetos, y aún no está programada para caminar, aunque su esposo y desarrollador afirmó que está trabajando en ello. El joven Zheng, que trabajó unos años en la multinacional tecnológica Huawei pero en 2014 abrió su propia compañía, aseguró que piensa vivir con Yingying hasta que la muerte -o los problemas de batería- les separe.
http://noticiasdelaciencia.com/not/22701/matematicas-para-esquivar-los-atascos-de-trafico/
Máquinas para fabricar teoremas matemáticos
Uno de los temores recurrentes ante el avance de la inteligencia artificial es la posible sustitución de los seres humanos por máquinas, dejándoles sin propósito más allá de las labores de mantenimiento de los robots. Si se introdujera todo el conocimiento disponible en una máquina, ¿podría resolver los grandes misterios de la disciplina, operando de forma mecánica a partir de las ideas ya conocidas? Uno de los primeros ejemplos se dio a mediados de los setenta, cuando los matemáticos Kenneth Appel y Wolfgang Haken demostraron el llamado teorema de los cuatro colores. Este, planteado en 1850, decía más o menos que cualquier mapa geográfico puede ser coloreado usando un máximo de cuatro colores diferentes, de forma que no queden regiones adyacentes con el mismo color. Appel y Haken fueron capaces de reducir el problema general a un número finito de casos concretos que había que comprobar haciendo una serie de cálculos. Pero, para verificar a mano los alrededor de 2.000 mapas, hubieran necesitado varias vidas, por lo que hicieron uso de la potencia de cálculo de un ordenador. En 1996, Neil Robertson, Daniel Sanders, Paul Seymour y Robin Thomas presentaron una nueva demostración asistida por ordenador del teorema de los cuatro colores. El artículo ocupaba 40 páginas, la implementación se realizó en código C (mucho más habitual y legible), y los mapas no se introducían de forma manual. En esta ocasión, otros investigadores sí pudieron reproducir la implementación de forma independiente, y fue aceptado. Por tanto, la verificación de este tipo de demostraciones no contradice el principio de revisión por pares. El uso del ordenador está lejos de ser una caja negra para producir incomprensibles demostraciones que se limitan a certificar la veracidad de un enunciado. Una demostración asistida por ordenador de un nuevo teorema eventualmente puede contener una idea inesperada o una nueva estrategia para inspirar investigaciones futuras.
¿Dónde están las mujeres matemáticas?
Resultado de imagen para mujeres matematicas
En el ámbito de la ciencia las mujeres han tenido que luchar por cada uno de sus derechos con trabajo y paciencia. Paradójicamente, determinadas situaciones de necesidad, como guerras, o las carreras espaciales frente al enemigo, han jugado a su favor. En esos momentos históricos se abrieron pequeñas rendijas que las mujeres aprovechaban para introducirse en las sociedades científicas, casi siempre de manera silenciosa y sin estruendos, pensando solo en el trabajo que realizaban. Este fue el caso de la matemática alemana Emmy Noether (1882-1935) cuyas contribuciones fueron determinantes en el desarrollo de la física moderna. Trabajó hasta convertirse en imprescindible en la evolución de la ciencia en su momento histórico, y esperó con paciencia a que sus colegas admiraran sus ideas y no tuvieran más remedio que aceptarla como una igual en la Universidad de Gotinga. En España, durante los años en que las mujeres lo tenían terriblemente difícil en la oscuridad de la dictadura franquista, la matemática gallega María Wonenburger (1927-2014) decidió moverse a universidades americanas y canadienses para perseguir su sueño: aprender y enseñar matemáticas. Primero intentó formar parte del Bryn Mawr College, precisamente donde reposan las cenizas de Emmy Noether, pero no lo consiguió. Pero con perseverancia consiguió convertirse en una de las primeras becadas Fullbright españolas. Mujeres como Wonenburger han pasado a la historia por ser “las primeras”. Junto a ella, Maryam Mirzakhani, galardonada medalla Fields en 2014 por sus importantes aportaciones en el estudio de los espacios de moduli de las superficies de Riemann, es la única mujer que ha obtenido hasta ahora este alto honor; la belga Ingrid Daubechies fue la primera presidenta de la Unión Matemática internacional; Anna Johnson Pell Wheeler, la primera mujer en impartir un Colloquium Lecture en 1927 en el congreso de la American Mathematical Society. Algunas de ellas, como en el caso de Mirzakhani, han dejado de ser “figuras ocultas” tras recibir un premio de la comunidad científica internacional que las ha hecho más visibles. Pero este se puede considerar un caso muy excepcional. Otras han recibido importantes galardones y son menos conocidas. Este es el caso de la iraní Sara Zahedi, premio de la Sociedad Matemática Europea por su excelente investigación sobre el desarrollo y análisis de algoritmos numéricos para ecuaciones en derivadas parciales con un enfoque en aplicaciones problemas con geometría dinámica. Y el de Sylvia Serfaty, premio Henri Poincaré, experta en ecuaciones en derivadas parciales y física matemática
Math2me, el canal del aprendizaje
Resultado de imagen para math2me
Math2me es un canal de youtube creado en 2009, el cuál te enseña a resolver diferentes problemas matemáticos. En este sitio podrás encontrar diferentes explicaciones a nivel primaria, secundaria y bachillerato. Asimismo, enseña a los estudiantes que utilizan su plataforma trucos, animaciones, curiosidades y reportajes para el uso de estas operaciones tanto en la escuela como en el área laboral. Tal ha sido el éxito de este concepto, que ya se ha extendido a diversos programas de televisión en varias ciudades de México al igual que en centros comunitarios, con la finalidad de difundir la educación a través de la tecnología.
Los creadores del portal, también han realizado traducciones de sus contenidos en videos de aritmética a la lengua mixteca en colaboración con asociaciones educativas. El canal cuenta con más de mil 900 videos con una duración en promedio de siete minutos, 120 millones de visitas en su canal, 520 mil suscriptores y más de 300 mil seguidores en sus redes. La herramienta educativa ha recibido diferentes premios, de los cuales destaca el Premio FRIDA en 2012, galardón que se otorga a iniciativas enfocadas en el desarrollo social y económico de América Latina y el Caribe.
El modelo matemático que explica la teoría keynesiana
Alfonso Ávila del Palacio, doctor en filosofía, especialista en matemáticas, profesor e investigador de la Universidad Juárez del Estado de Durango (UJED), en México, diseñó un modelo matemático para explicar la teoría económica keynesiana, que asegura que el Estado debe intervenir en el desarrollo de actividades económicas durante periodos de crisis. Ávila del Palacio. Explicó que Keynes, quien trabajó dentro de la teoría neoclásica de la economía, una corriente que se desarrolló en el mundo anglosajón, en Inglaterra originalmente, exponía que no existía el desempleo voluntario, ya que si alguien no encontraba trabajo era porque no aceptaba trabajos con salarios bajos, pero si alguien lo aceptaba, encontraba trabajo; pero surgió la Gran Depresión de 1929 que inició en Estados Unidos y se propagó al resto del mundo. Según la teoría neoclásica, no era posible que eso sucediera y como no se encontraban respuestas, Keynes se encargó de explicar por qué estaba pasando eso y la forma que se podía salir de esa crisis, refirió el doctor Ávila. Alfonso Ávila del Palacio Portada libro 3.jpg“Usando esas teorías (la de juegos y apuestas) me pareció que podía modelar la teoría de Keynes, mediante un juego en el que hay productores que están enfrentados de alguna manera a consumidores, y el tercer jugador es el Estado; la idea es que si dejamos solos a los productores y consumidores pueden llegar a una crisis, pero si interviene el gobierno, se puede evitar esa crisis”, precisó Ávila del Palacio.
La herramienta matemática de teoría de juegos, que utilizó, deriva de la teoría de probabilidades que inventó Pascal cuando un amigo le dijo en una noche de juegos que le hiciera una fórmula para ganar en los juegos de azar, y lo que hizo Pascal fue examinar las posibilidades, refirió el investigador. Finalmente, señaló que es necesario que las autoridades utilicen los resultados de investigaciones científicas y tecnológicas para respaldar las políticas públicas de México como una inversión a largo plazo para el desarrollo.
http://noticiasdelaciencia.com/not/23623/el-modelo-matematico-que-explica-la-teoria-keynesiana/
Asombrosa técnica para determinar con mayor
precisión sucesos en el tiempo
Digamos que estamos intentando identificar cuándo acaeció un suceso antiguo en particular, pero que nuestra mejor estimación lo sitúa solo dentro de un abanico de 10.000 años. Y ahora imaginemos que algo pudiera reducir esa ventana del “cuándo” a apenas 30 años.
Ese algo parece que ya existe y tiene esta potencia de resolución temporal. Se trata de una nueva herramienta matemática diseñada y probada por un equipo internacional de científicos, integrado, entre otros, por Abbas Ourmazd y Russell Fung, de la Universidad de Wisconsin-Milwaukee en Estados Unidos, así como Robin Santra y Oriol Vendrell, del Sincrotrón Alemán de Electrones (DESY, por sus siglas en alemán).
La herramienta, un algoritmo de aprendizaje automático, reduce las incertidumbres de datación durante sucesos cambiantes, mejorando la precisión en un factor de hasta 300.
Podría tener numerosas aplicaciones, desde datar con mejor precisión sucesos pasados de cambio climático a determinar cuándo se forman o se rompen los enlaces moleculares durante reacciones químicas que duran solo unas pocas milbillonésimas de segundo.
http://noticiasdelaciencia.com/not/19333/asombrosa-tecnica-para-determinar-con-mayor-precision-sucesos-en-el-tiempo/
De nuevo, un joven tapatío pone en alto el nombre de México en matemáticas
Desde Jamaica regresó con una medalla de oro en el cuello. Diego Hinojosa es un campeón: el joven tapatío de 15 años volvió a la ciudad hace apenas unos días con un logro educativo más, pues obtuvo la presea dorada en la pasada Olimpiada Matemática de Centroamérica y el Caribe, una competencia que tuvo lugar en la capital, Kingston. Estudiante de tercer grado de secundaria del Centro de Educación Integral Arboledas (Cedi) relata que en otras ocasiones participó en competencias similares en China y Argentina, sin embargo, no fue hasta su tercera participación que se hizo con la medalla de oro. La clave del éxito, confiesa, es la perseverancia. Este joven tapatío fue parte de la Selección Mexicana de Matemáticas, agrupación que compitió contra otros equipos de mayor edad, pues según Guillermo Rivera, delegado de la Olimpiada Nacional de Matemáticas, en el caso de México se les pide que sus participantes sean de menor edad que el resto, al ser uno de los países con mejores elementos en esta disciplina. Además, este tapatío busca derribar los tabúes acerca de la enseñanza de las matemáticas con uno de sus objetivos: enseñar y compartir los conocimientos obtenidos en estas competencias nacionales e internacionales y ampliar las perspectivas de las personas en torno a esta disciplina.
Matemáticas para esquivar los atascos de tráfico
Los atascos de tráfico, más allá de un quebradero de cabeza para los automovilistas, tienen un importante impacto social, económico y medioambiental. Ahora un equipo de investigadores de la Universidad Politécnica de Madrid (UPM), en España, ha desarrollado un algoritmo de toma de decisión que puede aplicarse a sistemas inteligentes de transporte para reducir las retenciones en las carreteras.
El algoritmo propuesto, cuya eficiencia ha sido validada en simulaciones, recomienda a los conductores el mejor itinerario en virtud de los datos de tráfico que proporciona la red de sensores desplegados en las principales vías de circulación.
El equipo de la UPM, perteneciente al Centro de Investigación en Tecnologías de Software y Sistemas Multimedia para la Sostenibilidad (CITSEM), se ha enfrentado a dos retos importantes para asegurar que la toma de decisiones sea fiable. Por un lado, la incertidumbre relacionada con los datos recibidos de los sensores, ya que la información puede ser incompleta, presentar inconsistencias o haber perdido precisión durante su medición, procesado y visualización. Por otro, la información del contexto obtenida por los sensores es variable, lo que obliga a que el algoritmo sea capaz de ajustar la toma de decisiones a esos cambios.
Los investigadores han adaptado para su trabajo uno de los algoritmos de toma de decisiones más utilizados, denominado Proceso Analítico Jerárquico -en inglés, Analytic Hierarchy Process (AHP)- , con el fin de emplearlo en los sistemas inteligentes de transporte teniendo en cuenta los retos antes mencionados.
Para ello, han fusionado dos variantes de ese algoritmo: FAHP y DAHP. En la primera, se utiliza la lógica difusa para realizar los cálculos atendiendo al efecto de la incertidumbre en los datos recibidos; en la segunda, las variables utilizadas en los cálculos se consideran dinámicas y, por tanto, variables con el tiempo.
http://noticiasdelaciencia.com/not/22701/matematicas-para-esquivar-los-atascos-de-trafico/
Yves Meyer y sus ondículas reciben el ‘nobel’
de matemáticas
El presidente de la Academia Noruega de Ciencias y Letras, Ole M. Sejersted, anunció el 21 de marzo el ganador del Premio Abel 2017: el matemático francés Yves Meyer, de L’École normale supérieure Paris-Saclay.
Nacido hace 77 años en el seno de una familia sefardí y educado en Túnez y Francia, Meyer ha sido “el líder visionario” en el moderno desarrollo de la teoría de las ondículas, unas funciones o pequeñas oscilaciones que se encuentra en la intersección entre las matemáticas, la tecnología de la información y las ciencias de la computación.
El término original francés ondelette (traducido como wavelet en inglés y ondícula en español) fue introducido por el geofísico Jean Morlet y el físico teórico Alex Grossmann, cuyo trabajo conoció Meyer por unos papeles que le enseñaron en 1984 mientras esperaba su turno en una fotocopiadora, según cuenta en una entrevista a Mathematics-in-Europe: “Después tomé el primer tren a Marsella para encontrarme con ellos (y la matemática Ingrid Daubechies). Fue como un cuento de hadas. Me enamoré del procesamiento de señales. Sentí que por fin había encontrado mi hogar".
Tras haber hecho importantes contribuciones en el campo de la teoría de números a principios de su carrera, la energía y curiosidad ilimitadas de Meyer lo incitaron a trabajar en métodos destinados a dividir objetos matemáticos complejos en componentes de estructura más simple similares a las ondas; una materia denominada análisis armónico. Esto, a su vez, le llevó a ayudar a construir una teoría destinada al análisis de señales complicadas, con importantes consecuencias para la informática y las tecnologías de la información.
http://noticiasdelaciencia.com/not/23553/yves-meyer-y-sus-ondiculas-reciben-el-lsquo-nobel-rsquo-de-matematicas/
Otorgan el 'Nobel de matemáticas' a John Nash y Louis Nirenberg
Por sus estudios en el área de la teoría de ecuaciones diferenciales no lineales parciales, el estadounidense John F. Nash Jr y el canadiense Louis Nirenberg fueron distinguidos este miércoles con el premio Abel, considerado el ‘Nobel de las matemáticas’.
Nash, de 86 años, ganó en 1994 el Nobel de Economía por su teoría de los juegos, y es conocido también por inspirar la película ‘Una mente maravillosa’ (2001), que narra su lucha contra la esquizofrenia.
La Academia de las Ciencias y las Letras noruega destacó en el fallo, difundido este miércoles en Oslo, las contribuciones "sorprendentes y seminales" de ambos y las aplicaciones de estas en el análisis geométrico.
Sus teorías son usadas también para describir leyes fundamentales dentro de la física, la química o la biología y pueden servir para explicar fenómenos como las colas del tráfico, la circulación sanguínea o los tsunamis.
Campeona de matemáticas se reúne con Aristóteles
Olga Medrano Martín del Campo, ganadora de la medalla de oro en la Olimpiada Europea de Matemática femenil, sostuvo un encuentro con el gobernador, Aristóteles Sandoval. En la reunión el mandatario estatal consideró a la joven como un ejemplo nacional, pero particularmente para Jalisco y para que otros estudiantes puedan esforzarse y alcanzar sus metas.
Durante el encuentro, realizado en Casa Jalisco, el mandatario estatal ofreció a la joven todo el apoyo y respaldo del Gobierno del Estado para que la campeona, quien tiene 17 años, pueda consolidar una exitosa trayectoria y así replicar su experiencia en beneficio de niños y jóvenes jaliscienses.
Estudiante tapatío destaca en Olimpiada de Matemáticas en Rumania
GUADALAJARA, JALISCO (14/ABR/2016).- Leonardo Ariel García Morán, estudiante de preparatoria de la Universidad del Valle de México (UVM), campus Guadalajara Norte, obtuvo mellada de plata al representar a México en el Máster de Matemáticas de Rumanía.
En un comunicado, la UVM informó que el alumno, de 16 años edad, que cursa el cuarto semestre de preparatoria, presentó durante la competencia dos exámenes donde resolvió problemas sobre geometría, álgebra, teoría de números y combinatorias.
Leonardo inició su trayectoria como campeón de matemáticas cuando cursaba el último año de secundaria, donde recibió la invitación para participar en el concurso de matemáticas del estado de Jalisco y a partir de éste, se preparó y continuó compitiendo en Olimpiadas a nivel nacional e internacional.
Cómo usar el fútbol para enseñar matemáticas a los niños
Si la montaña no va a Mahoma, Mahoma va a la montaña.
Este dicho fue seguido por las autoridades rumanas para tratar de solucionar el problema que están sufriendo en las escuelas, tanto por el bajo nivel académico como por el alto número de niños que abandonan los estudios.
Fue así que implementaron una peculiar idea al cambiar el tradicional pizarrón de las aulas por el uniforme de entrenamiento de la selección nacional de fútbol.
De esta manera, aprovechando el alcance e influencia del deporte más popular del país, se colocó una operación matemática en la espalda de cada jugador con el objetivo de familiarizar a los aficionados con símbolos básicos como suma, resta, multiplicación y división.
"Fútbol y matemáticas no son excluyentes", explicó Razvan Burleanu, presidente de la Federación Rumana de Fútbol, país que clasificó a la Eurocopa que se disputará en Francia entre los próximos meses de junio y julio. "Debemos ver el deporte y la educación no sólo como elementos complementarios, sino fundamentales en la integración en la preparación y perfeccionamientos de los niños". El 18% de la población escolar en Rumanía no terminan los estudios, lo que representa uno de los peores índices de toda la Unión Europea.
EL PROBLEMA DE LAS OCHO DAMAS
Seguramente el problema ajedrecista más famoso y analizado de todos los tiempos, que atrajo la atención del mismísimo Gauss, el príncipe de los matemáticos.
El problema de las ocho damas, propuesto la semana pasada, fue planteado por primera vez por el ajedrecista alemán Max Bezzel; que, con el seudónimo Schachfreund, lo publicó en 1848 en la revista especializada Berliner Schachzeitung. Puesto que la dama puede desplazarse horizontal, vertical o diagonalmente. El problema equivale a situar ocho fichas en el tablero de forma que no haya dos en la misma fila, columna o diagonal (lo cual emparenta con el popular sudoku).
El problema de las ocho damas fue analizado, entre otros, por el mismísimo Gauss; que halló 76 de las 92 soluciones posibles. pero el primero en encontrarlas todas, en 1850, fue un amigo suyo; el matemático ciego Franz Nauck.
http://elpais.com/elpais/2016/03/10/ciencia/1457629302_411493.html
En un comunicado, la UVM informó que el alumno, de 16 años edad, que cursa el cuarto semestre de preparatoria, presentó durante la competencia dos exámenes donde resolvió problemas sobre geometría, álgebra, teoría de números y combinatorias.
Leonardo inició su trayectoria como campeón de matemáticas cuando cursaba el último año de secundaria, donde recibió la invitación para participar en el concurso de matemáticas del estado de Jalisco y a partir de éste, se preparó y continuó compitiendo en Olimpiadas a nivel nacional e internacional.
De esta manera, aprovechando el alcance e influencia del deporte más popular del país, se colocó una operación matemática en la espalda de cada jugador con el objetivo de familiarizar a los aficionados con símbolos básicos como suma, resta, multiplicación y división.
LAS MATEMÁTICAS Y EL LENGUAJE PRODUCIRÍAN DIFERENTES REDES NEURONALES
Lo sugiere un estudio realizado en universidades francesas
La conclusión de los autores es que el cerebro humano tiene diferentes redes neuronales para el procesamiento de las habilidades matemáticas y para el lenguaje , pero cuando se trata de entender las matemáticas de una manera básica utiliza la misma red neuronal, sin importar si es experto o no.
La población mundial alcanzará los 11.000 millones en 2100
Un equipo de demógrafos y expertos en estadística de la ONU y la Universidad de Washington ha utilizado las últimas herramientas de estadística para elaborar un estudio en el que se afirma que la población mundial no solo no se estancará, sino que crecerá hasta los 11.000 millones a finales de este siglo.
Esta cifra supone 2.000 millones de habitantes más que lo que se había calculado en estudios previos, según se asegura en este trabajo, que se publica en el último número de Science.
“El consenso entre los expertos durante los últimos veinte años era que la población mundial, que ahora es de 7.000 millones de habitantes, alcanzaría los 9.000 millones y luego se estabilizaría o probablemente entraría en declive", explica Adrian Raftery, profesor de estadística y sociología de la Universidad de Washington y uno de los autores del estudio.
Sin embargo –añade– “hemos encontrado que hay un 70% de probabilidad de que la población no se estabilice en este siglo”.
http://noticiasdelaciencia.com/not/11461/la-poblacion-mundial-alcanzara-los-11-000-millones-en-2100/
Una fórmula matemática para la felicidad
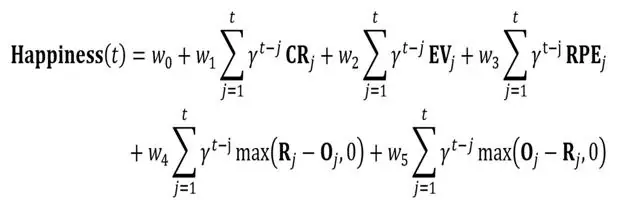La felicidad momentánea de más de 18.000 personas de todo el mundo se ha podido predecir con éxito mediante una ecuación matemática ideada por investigadores del University College de Londres (UCL).
Los resultados del trabajo, que ha publicado la revista PNAS, muestran que el estado de ánimo feliz se relaciona no solo con el hecho de que las cosas vayan bien, sino que lo hagan mejor de lo esperado.
La investigación arrancó pidiendo a 26 personas que realizaran una tarea de toma de decisiones, de tal forma que sus respuestas determinaban ganancias o pérdidas monetarias. En cada momento se les preguntaba por su nivel de felicidad, además de medir su actividad neuronal mediante imágenes de resonancia magnética funcional.
Un modelo matemático para optimizar el uso de la madera
A lo largo de la historia de la construcción, la madera ha sido uno de los materiales usados por excelencia. Con el paso del tiempo, otros elementos la han desplazado, sin embargo, sigue siendo el material más utilizado en las construcciones de bajo presupuesto. En Chile, la industria forestal se ha desarrollado ampliamente, llegando a un 2,6 por ciento del producto interno bruto (PIB) y la madera se impuso como tercer producto chileno más exportado el 2011, según la Corporación Chilena de la Madera.
Pese a la importancia de este producto a nivel mundial, existen pocas investigaciones sobre la madera, manteniéndose muchas dudas sobre sus propiedades y atributos.
“A la fecha no se entiende completamente, ni en Chile ni el mundo, cómo predecir con exactitud las propiedades mecánicas y capacidades resistentes de la madera. Eso, de alguna forma, se traduce en ciertas deficiencias en el diseño de estructuras, siendo utilizada de forma conservadora, lo que significa un uso de más material que lo óptimo”, señala el académico del Departamento de Ingeniería en Obras Civiles, Dr. Erick Saavedra, indicando que su estudio puede ser un aporte en la materia.
Las matemáticas de Turing explican la formación de los dedos
El científico británico Alan Turing (1912-1954) contribuyó a la biología matemática con la publicación, en 1952, de un solo un artículo (The Chemical Basis for Morphogenesis, en Philosophical Transactions of the Royal Society of London) que provocó el desarrollo de toda una nueva área de investigación relacionada con la creación de patrones en la naturaleza.
El matemático descubrió un sistema de dos moléculas que podían, al menos en teoría, crear patrones de manchas o de rayas si las moléculas se difundían e interactuaban químicamente de una determinada manera. Las ecuaciones matemáticas mostraban que, partiendo de una condición de uniformidad, estas moléculas podrían autoorganizar su concentración de manera espontánea en un repetitivo patrón.
Ahora, un grupo de investigadores del laboratorio de Biología de Sistemas Multicelulares del Centro de Regulación Genómica (CRG), coordinados por James Sharpe, coautor del estudio, ha conseguido los tan anhelados datos suficientes para confirmar que los dedos de manos y pies siguen el modelo descrito por el mecanismo de Turing.
Una técnica matemática abandonada del siglo XIX “resucita” para la computación moderna
Una reliquia de mucho antes de la época de la , la estrategia matemática de 169 años de antigüedad conocida como método iterativo de Jacobi, es hoy en día ampliamente rechazada por ser demasiado lenta para ser útil. Pero gracias a unos científicos, esta técnica podría recibir pronto un nuevo impulso vital.
Con apenas unos pocos retoques para actualizarla, el equipo de Rajat Mittal y Xiang Yang, de la Universidad Johns Hopkins en Baltimore, Maryland, Estados Unidos, ha conseguido hacer que la casi olvidada técnica de Jacobi funcione hasta 200 veces más rápido.
El resultado podría aumentar el rendimiento de las simulaciones por ordenador utilizadas en el diseño aeroespacial, la construcción de buques, el modelado meteorológico y climático, la biomecánica y otras tareas de ingeniería.
Complejos modelos matemáticos mejoran la fluidez del tráfico
El grupo Automática y Robótica industrial, liderado por el catedrático de ingeniería de Sistemas y Automática de la Universidad de Sevilla (US) Eduardo Fernández Camacho, propone soluciones a los problemas de tráfico denso mediante el uso de control predictivo y modelos dinámicos complejos.
Estos modelos, que son útiles no sólo para mejorar la gestión de infraestructuras, sino también para su utilización en aplicaciones biomédicas o de la industria petroquímica, se basan en ecuaciones diferenciales parciales que en el caso del tráfico describen la relación que hay entre el flujo y la densidad o la velocidad.
“Un sistema complejo está compuesto por diferentes subsistemas difíciles de tratar ya que dependen de numerosas variables”, explica el catedrático, que añade: “El tráfico es un ejemplo de este tipo de sistemas debido a que su dinámica depende de muchos factores: desde la meteorología a los días festivos, pasando por la personalidad de los propios conductores”.
Un algoritmo clasifica películas mejor que críticos expertos
Investigadores de la Universidad Northwestern de Illinois (EEUU), han creado un método automatizado para medir el interés artístico que es capaz “de asignar el grado de relevancia de una película con mayor facilidad y exactitud que críticos de cine y que, además puede ser utilizado en otros campos como el científico” explica a Sinc Luís A. Nunes Amaral, científico portugués que codirige el Instituto de Sistemas Complejos de la universidad estadounidense. El trabajo ha sido publicado en la revista Proceedings of National Academy of Science (PNAS).
Su afirmación se basa en la coincidencia entre los datos obtenidos con este método y las películas incluidas en el Registro Nacional de Cine de la biblioteca del Congreso de los Estados Unidos. Aquí se encuentran las obras de más de 10 años de antigüedad que son relevantes por su valor cultural, histórico o estético, según la opinión de un comité de expertos multidisciplinares.
A la hora de medir objetivamente la relevancia de un filme, los investigadores contemplaron tres factores: la calidad, el impacto y la influencia.
http://www.agenciasinc.es/Noticias/Un-algoritmo-clasifica-peliculas-mejor-que-criticos-expertos
Un algoritmo aprende de sus malas decisiones para ser imbatible en póquer
Un programa informático, denominado Cepheus, es capaz de pasar una vida humana jugando al póquer sin que nadie logre vencerlo. Investigadores de la Universidad de Alberta (Canadá) han creado un algoritmo que permite resolver por primera vez juegos en forma extensiva y con información imperfecta, como la versión más extendida del póquer: Limit Texas Hold'em. Los resultados del estudio se han publicado en el último número de la revista Science.
Según la teoría de juegos, el póquer es un juego de información imperfecta, lo cual significa que los datos que manejan los jugadores no son conocidos por el resto, con el añadido de que incluso pueden ser falsos si el jugador se marca un farol.
“Cepheus ha creado y desarrollado su propia estrategia desde cero, únicamente conociendo las normas del juego. El resultado son más de 260 terabytes de información, 1.000 veces más que lo que ocupa la versión en inglés de la Wikipedia”, explica a Sinc Michael Bowling, investigador de la universidad canadiense y uno de los desarrolladores del programa.
http://www.agenciasinc.es/Noticias/Un-algoritmo-aprende-de-sus-malas-decisiones-para-ser-imbatible-en-poquer
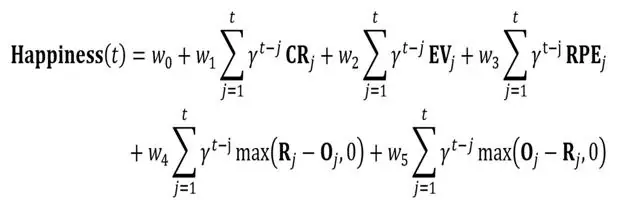
Los monos también tienen habilidades matemáticas
El experimento al que fueron sometidos estos animales consistió en mostrarles diferentes números de puntos en la pantalla de una computadora, estos aumentaban, disminuían o permanecían idénticos y si esto último sucedía, el mono debía accionar una palanca y recibía una recompensa. Los descubrimientos de los investigadores demuestran que los monos, al igual que el ser humano, pueden evaluar cantidades, siendo capaces de diferenciar mejor grupos de puntos que están más alejados entre sí.
“Las matemáticas ayudan en la defensa frente al terrorismo”
.gif){kind=link}
Un simulador matemático precide resultados de béisbol y fútbol americano
.gif){kind=link}
.gif){kind=link}
.gif){kind=link}
“El móvil permite estudiar el comportamiento humano a un nivel espacial, temporal y social sin precedentes”
Logran predecir las interacciones entre células cancerosas usando la Teoría de Juegos
Unos investigadores han conseguido predecir las interacciones entre células cancerosas valiéndose de la Teoría de Juegos, en lo que constituye una demostración más de la versatilidad de esta herramienta matemática a la que se ha recurrido con éxito en campos muy variados, desde la biología a la economía, e incluso para desarrollar modelos matemáticos con los que ayudar a resolver problemas de congestión administrativa en una corte de justicia, como por ejemplo hizo brillantemente el matemático Ricardo Miró.
El equipo de Gerhard Christofori, profesor en el Departamento de Biomedicina de la Universidad de Basilea en Suiza, se valió de una parte de la Teoría de Juegos que se ha empleado a menudo en economía, como modelo para analizar la provisión de bienes comunes.
Nueva teoría matemática para explicar los intrigantes patrones de las huellas dactilares y otras arrugas de la naturaleza
Un teorema de Pitágoras de hace 2.500 años halla un uso actual en análisis médicos
Los números tienen diferentes clasificaciones, y el número 5 puede englobarse varias: es un número primo; pentagonal; número de Catalán; número piramidal cuadrado; número cuadrado perfecto; número de Bell y número de la sucesión de Fibonacci.
Ocurrió, sin embargo, una tragedia. Cuando el segundo y último volumen de la obra ya se encontraba en prensa, Frege recibió una carta de Bertrand Russell, filósofo de la Universidad de Cambridge. Tras unas cuantas líneas en las que elogiaba el trabajo de Frege, la carta señalaba «una dificultad». Esa dificultad se conoce hoy con el nombre de paradoja de Russell. Sus consecuencias pueden compararse a la detonación de una bomba nuclear en los cimientos de la teoría de Frege.
Para explicar de qué trata la paradoja, primero necesitamos describir el proyecto de Frege. En terminología contemporánea, lo que Frege había construido era una teoría de conjuntos. Un conjunto consiste en una colección de objetos. El conjunto de los elefantes, por ejemplo, es una entidad matemática que tiene como miembros a todos los elefantes y solo a ellos; el conjunto de los volcanes se encuentra formado por todos los volcanes y solo por ellos.
En la investigación, los bebés oían una voz que numeraba hasta seis mientras un vídeo mostraba una mano que iba bien señalando por turno los peces de un grupo de seis, o bien moviéndose entre dos de los peces. Los niños dedicaron más tiempo a observar las secuencias en las que la voz en off y la mano en pantalla enumeraban los peces de forma correcta, comportamiento que reflejaba su preferencia. Por tanto, sabían cómo llevar la cuenta. «Los pequeños tienen mucha más conciencia de los objetos de lo que suele creerse», afirma Siegal.
Un buen número de fenómenos económicos responde a lo que en física se conoce bajo el nombre de dinámica no lineal o dinámica de sistemas complejos: sistemas cuyo comportamiento colectivo no se puede explicar a partir de la simple superposición de sus partes constituyentes.
Escoja una fila o columna y teclee en orden los tres números que la componen; después, introduzca los mismos números, pero en el orden inverso. Si ha escogido la segunda columna, por ejemplo, su número será el 852.258, y si se ha decidido por la tercera fila, el 123.321. Una vez aparezca su número en pantalla, divida entre 37. Ahora, utilizaré todos mis poderes de concentración para predecir si su resultado incluye o no un residuo decimal. ¿Ya tiene el número y lo ha dividido entre 37? Bien: vaticino que su resultado no contiene cifras decimales. Sorprendente, ¿no es cierto?
http://www.investigacionyciencia.es/investigacion-y-ciencia/numeros/2011/5/ilusionismo-matemtico-8393
NUNCA DIGAS NUNCA
MATEMÁTICAS PARA LA E-DEMOCRACIA
Los expertos están de acuerdo en la existencia de una especie de la segunda ley de la termodinámica de las relaciones de pareja, según la cual hace falta un cierto esfuerzo para mantenerse juntos, según explica Rey en un artículo publicado en la revista PLos One. Según sus resultados, mantener el amor a largo plazo "es algo muy costoso y, con excepciones, casi imposible". "El dicho popular de que el amor no es suficiente se cumple y sugiere que la "erosión" de las relaciones debe prevenirse de algún modo".
POR QUÉ TODA CLASIFICACIÓN ES IMPERFECTA
Pongámonos en el lugar de Mark Zuckerberg cuando puntuó y clasificó a las estudiantes de Harvard en Facemash, el predecesor de Facebook. El método más sencillo habría consistido en pedir a la gente que votase a su favorita y, después, otorgar a cada estudiante tantos puntos como número de votos recibidos. Sin embargo, en muy raras ocasiones son todos los votos iguales: en general, el de alguien desinformado no resultará tan valioso como el de un experto. En el caso de Facemash, el sexo de los votantes seguramente desempeñase algún papel.
DE LOS UNIVERSOS DIGITALES A LA MENTE
![[Img #19049]](https://images-blogger-opensocial.googleusercontent.com/gadgets/proxy?url=http%3A%2F%2Fnoticiasdelaciencia.com%2Fupload%2Fimg%2Fperiodico%2Fimg_19049.jpg&container=blogger&gadget=a&rewriteMime=image%2F*){kind=link}
A los 50 minutos de vuelo y sin que se diera ninguna señal de alarma, se perdió todo contacto con la aeronave, que en ese momento estaba sobrevolando el Mar de China Meridional, al sur de la península Ca Mau de Vietnam.
Lo que siguió fueron 17 días de misterio y especulaciones. Las tareas de rescate movilizaron a 26 países, incluidas potencias internacionales como China, Japón y Estados Unidos, que en una carrera contra reloj buscando posibles sobrevivientes, rastrearon las distintas rutas posibles.
A pesar del despliegue de tanta tecnología, no fueron ni los 29 aviones, 18 barcos o 6 helicópteros los que dieron con los restos del avión, sino uno de los 21 satélites a los que se pidieron informes. Específicamente, el de la compañía inglesa Inmarsat, en órbita desde 1990. Los créditos, sin embargo, no se los debe llevar la tecnología espacial sino la mente humana de los ingenieros que aplicaron teorías de la física y la matemática para decodificar las señales captadas satelitalmente.
Insólito – Resuelve raíz decimotercera de un número de 200 dígitos en 70 segundos
El francés Alexis Lemaire, de 27 años, volvió a derrotar a las calculadoras más avanzadas y quebró el martes en Londres su propio récord, al resolver la raíz decimotercera de un número de 200 dígitos en sólo 70 segundos.
En una prueba desarrollada en el Museo de Ciencias de Londres, el atleta matemático calculó la raíz decimotercera de un número de 200 dígitos con sólo el poder de su cerebro en apenas 70,2 segundos, quebrando su récord anterior de 72,4 segundos.
http://www.planetacurioso.com/categoria/curiosidades-matematicas/
UN MODELO ESTADÍSTICO PREDICE EL NÚMERO DE GOLES DE CADA FUTBOLISTA
![[Img #13775]](https://images-blogger-opensocial.googleusercontent.com/gadgets/proxy?url=http%3A%2F%2Fnoticiasdelaciencia.com%2Fupload%2Fimg%2Fperiodico%2Fimg_13775.jpg&container=blogger&gadget=a&rewriteMime=image%2F*){kind=link}
Su trabajo, publicado en el European Journal of Sport Science, presenta un modelo basado en la estadística bayesiana que, según ellos, sirve para predecir el número de goles que marcará cada jugador en función de sus propias cualidades individuales.
Como explican los investigadores, el hecho de que un jugador marque un gol depende de factores extrínsecos fácilmente cuantificables, como el número de minutos o partidos jugados, la posición en el campo –defensa, centrocampista o delantero– y la calidad del equipo (medida por su posición en la tabla clasificatoria). Pero no solo depende de esto.
![[Img #18527]](https://images-blogger-opensocial.googleusercontent.com/gadgets/proxy?url=http%3A%2F%2Fnoticiasdelaciencia.com%2Fupload%2Fimg%2Fperiodico%2Fimg_18527.jpg&container=blogger&gadget=a&rewriteMime=image%2F*){kind=link}
Esta investigación ha sido publicada en la revista especializada internacional Journal of Pattern Recognition Letters bajo el título Detección de líneas en imágenes con distorsión: Aplicación para la corrección de la distorsión (Line detection in images showing significant lens distortion and application to distortion correction). El trabajo persigue detectar de forma automática las líneas rectas en imágenes que experimentan gran distorsión (radial). Para ello, los investigadores amplían la transformada clásica de Hough (técnica para la detección de figuras en imágenes digitales), incluyendo un parámetro de distorsión que permite extraer con mayor fiabilidad las líneas rectas en la imagen distorsionada.
Crece 40% ciberdelito en México
http://noticiasdelaciencia.com
El problema de las matemáticas más difícil de resolver
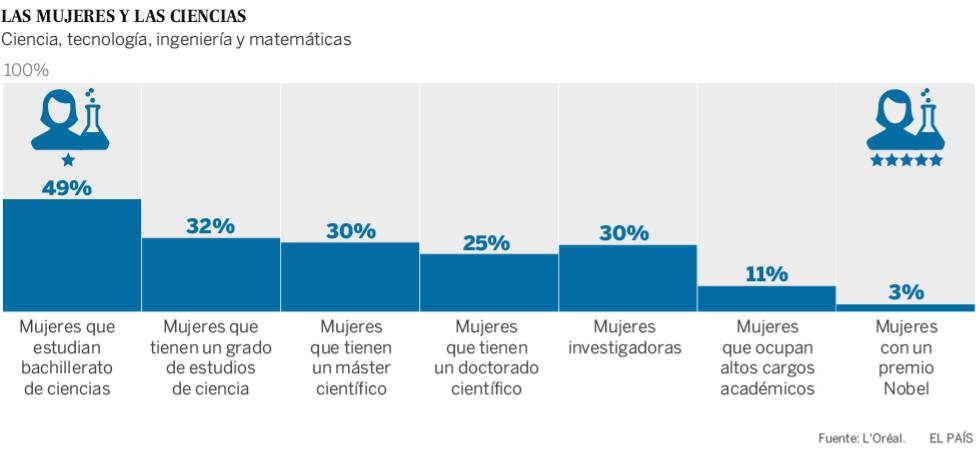
Matemáticas para responder ante un tsunami
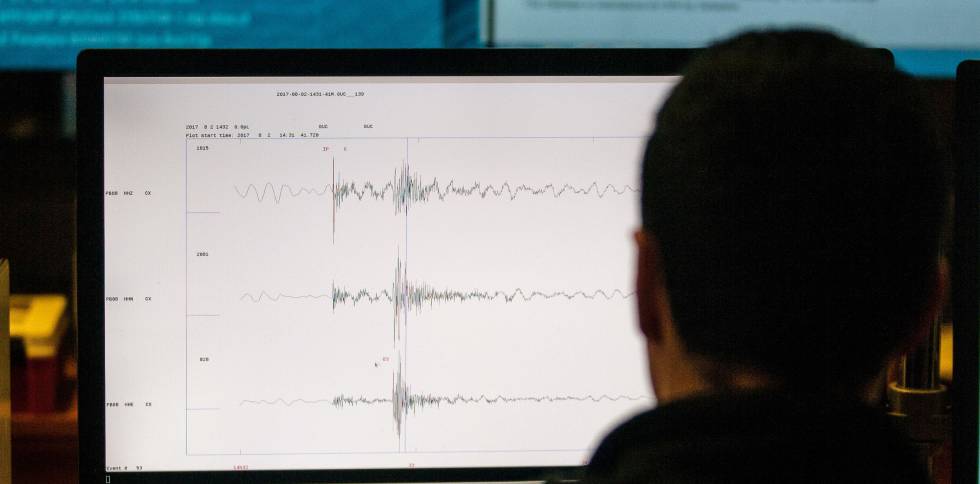
Día de la mujer calculadora
DESTACAN MEXICANAS EN OLIMPIADA EUROPEA FEMENIL DE MATEMÁTICAS 2019
- Las estudiantes de bachillerato consiguieron un oro, dos platas y una mención honorífica
- Contendieron 200 participantes de 49 países, en Kiev, Ucrania
